10  机器学习方法应用财务数据

10.1 批量筛选优质上市公司

各位同学，欢迎来到《商业大数据分析与应用》的全新章节。在之前的学习中，我们已经掌握了如何利用Python对单一公司进行深入的趋势分析和同业分析。今天，我们将把这些技能整合与升华，学习如何自动化、批量地对一个完整行业（以白酒行业为例）的所有上市公司进行综合评价，最终筛选出我们心目中的“优质公司”。这不仅是技能的综合运用，更是将数据分析能力转化为投资决策洞察力的关键一步。

10.1.1 核心评价框架

要批量筛选优质公司，我们首先需要一个清晰、量化的评价框架。这个框架将结合我们之前学过的两大分析维度：趋势分析与同业分析。

• 趋势分析：这相当于企业与自身的“历史”对话。通过分析公司过去几年的财务指标变化趋势，我们可以判断其发展轨迹是蒸蒸日上还是停滞不前。一个持续向好的趋势通常是公司内生增长动力强劲的体现。

• 同业分析：这则是企业在“行业赛道”上的横向比较。一家公司的财务指标即便趋势向好，也需要与竞争对手比较才能判断其真实水平。例如，在行业普遍高速增长的背景下，一家公司的增长率若低于行业平均，可能就不是一个好的信号。

10.1.1.1 评价指标体系

我们的综合评价体系将建立在一系列经典的财务指标之上，这些指标覆盖了衡量一家公司经营状况的四个核心维度。同时，我们还将引入现金流量表中的关键指标，以更全面地评估公司的“造血能力”和财务健康状况。

1. 盈利能力：企业赚钱的本领。
   • 核心指标：毛利率、营业利润率、净利润率、净资产收益率(ROE)。
2. 营运能力：企业利用资产创造收入的效率。
   • 核心指标：存货周转率、总资产周转率、应收账款周转率。
3. 偿债能力：企业偿还债务、抵御财务风险的能力。
   • 核心指标：流动比率、速动比率、利息保障倍数。
4. 成长能力：企业在未来扩大规模、提升利润的潜力。
   • 核心指标：营业收入增长率、营业利润增长率、净利润增长率。
5. 现金流健康度：企业经营活动的“血液循环”是否通畅。
   • 核心指标：经营活动产生的现金流量净额/净利润、销售商品/提供劳务收到的现金/营业收入、期末现金及现金等价物余额/有息负债。

10.1.1.2 综合评分模型

为了得到一个最终的、可供排序的综合分数，我们将对趋势分析和同业分析的结果进行加权平均。权重的设定反映了我们对不同分析维度的重视程度。在本案例中，我们设定如下权重：

• 趋势分析得分：权重 40%
• 同业分析得分：权重 60%

这个权重分配意味着我们认为，一家公司在行业中所处的相对位置（同业分析）比其自身的发展趋势（趋势分析）稍微更重要一些。当然，这个权重是主观的，在真实的商业决策中，分析师会根据自己对行业的理解和投资策略来调整。例如，对于一个新兴、快速变化的行业，可能会更看重成长趋势；而对于一个成熟、格局稳定的行业，则可能更看重其在同业中的竞争地位。

10.1.2 Python实战：批量评价白酒行业公司

接下来，让我们进入激动人心的实战环节。我们将编写一个Python脚本，自动完成以下任务： 1. 获取A股所有白酒行业的上市公司名单。 2. 对每家公司，基于过去数年的财务数据，计算其“趋势得分”。 3. 对每家公司，计算其在整个行业中的“同业得分”。 4. 根据我们设定的权重（趋势40%，同业60%）计算最终的“综合得分”。 5. 输出白酒行业上市公司的综合排名。

10.1.2.1 数据准备与环境设置

首先，我们需要导入所有必需的Python库，并使用Tushare Pro的API获取上市公司基本信息。请确保你已经配置好了自己的Tushare密钥。

如 列表 lst-get-baijiu-stocks 所示，我们首先获取所有A股上市公司的基本信息，然后通过industry字段筛选出所有属于“白酒”行业的公司。

列表 10.1

## 导入相关库
import pandas as pd
import numpy as np
import tushare as ts
import time
import warnings;warnings.simplefilter("ignore")

## 输入tushare密钥
pro = ts.pro_api('ba1646815a79a63470552889a69f957f5544bef01d3f082159bf8474')

## 获取同行业股票代码
com_data = pro.stock_basic(exchange='', list_status='L', 
fields='ts_code,symbol,name,area,industry,list_date')
## 要求1: 筛选出白酒行业的公司
bj_com = com_data[com_data['industry'] == '白酒']

## 将筛选出的公司代码和名称转换为列表，方便后续循环调用
bj_code = bj_com['ts_code'].tolist()
bj_name = bj_com['name'].tolist()

## 定义分析的年份范围
years =

## 要求2: 手动修正部分公司名称以匹配本地文件名（此为数据清洗的常见步骤）
bj_name = "皇台酒业"

关于数据预处理

在 列表 lst-get-baijiu-stocks 中，我们手动修改了列表中的一个公司名称。这是一个非常典型的实际数据处理场景。因为API返回的官方名称可能与我们本地存储的文件名（例如，*ST皇台 vs 皇台酒业）有细微差别，导致程序无法正确读取文件。在实际项目中，编写更鲁棒的名称匹配逻辑是数据清洗的重要一环。

10.1.2.2 计算趋势得分

现在我们开始对列表中的每一家公司进行循环，计算其趋势得分。基本逻辑是：对于每一个财务指标，我们检查其逐年变化趋势。如果指标是“越高越好”型（如ROE），那么逐年递增则加分；反之，如果是“越低越好”型，则逐年递减才加分。在我们的评分体系中，所有选用的指标都是前者，因此我们统一判断指标是否逐年提升。

列表 lst-trend-scoring 的代码会遍历bj_name列表中的每个公司，读取其预先计算好的财务比率表，然后逐个指标进行历年比较并评分，最后将所有指标的平均分作为该公司的“趋势评分”。

列表 10.2

## 首先设置一个设置好行索引的空表，用于存放后续计算结果
## 我们以贵州茅台的数据为模板创建一个空的DataFrame结构
score_sheet_trend = pd.read_excel('贵州茅台_2019'+'.xlsx',sheet_name = '财务比率表').rename(columns={'Unnamed: 0': '公司名称'}).set_index('公司名称').iloc[:,0:0]

## 遍历所有白酒公司名称
for comp in bj_name:
  # 读取该公司的财务比率表数据
  df_ratio = pd.read_excel(comp+'_2019.xlsx',sheet_name='财务比率表')
  # 重命名首列并将其设为索引，方便处理
  df_ratio = df_ratio.rename(columns={'Unnamed: 0': '公司名称'}) 
  df_ratio = df_ratio.set_index('公司名称')
  # 将数据转置，使得年份为行，指标为列，便于按时间序列比较
  data = df_ratio.T
  
  # 进行评分
  scores = []
  # 遍历每一个财务指标 (data.T的每一行)
  for i in range(len(data.T)):
    n = 0
    # 遍历每一年 (data的每一行)，比较j年和j+1年的数据
    for j in range(len(data)-1):
      # 要求3: 判断是否为无穷大，若是则加分
      if np.isinf(data.iloc[j,i]) == True:
        n = n+1
      # 如果指标值逐年改善 (这里是增长)，则加分
      elif data.iloc[j,i]>data.iloc[j+1,i]:
        n = n+1
    # 分数标准化为100分制
    n = n/(len(data)-1) * 100
    scores.append(n)
    
  # 将计算出的该公司所有指标的得分列表存入结果表中
  score_sheet_trend[comp] = scores

## 将结果表转置，让公司名为行，指标为列
score_sheet_trend = score_sheet_trend.T
## 计算每个公司所有指标的平均分，作为最终的趋势评分
trend_scores = round(score_sheet_trend.T.mean(),2)
score_sheet_trend['趋势评分'] = trend_scores

10.1.2.3 计算同业得分

同业得分的计算逻辑与趋势得分不同。它衡量的是在某一个时间点上（本案例中使用的是各公司过去几年的平均值），一家公司的某个财务指标在整个行业中所处的位置。我们使用分位数来进行评分：

• 指标值高于行业75%分位数：得100分（优秀）
• 指标值介于行业50%与75%分位数之间：得75分（良好）
• 指标值介于行业25%与50%分位数之间：得50分（中等）
• 指标值低于行业25%分位数：得25分（较差）

列表 lst-peer-scoring 代码块首先会计算出整个行业在各个指标上的分位数（25%, 50%, 75%），然后遍历每家公司，将其指标值与行业分位数进行比较，从而给出同业评分。

列表 10.3

## 创建一个空的DataFrame用于存储每个公司各指标的均值
ratio_ind = pd.DataFrame()
for name in bj_name:
  # 读取财务比率表数据
  df_ratio = pd.read_excel(name+'_2019.xlsx',sheet_name='财务比率表')
  df_ratio = df_ratio.rename(columns={'Unnamed: 0': '公司名称'})  
  df_ratio = df_ratio.set_index('公司名称')
  # 计算该公司各指标在过去几年的平均值
  meanvalue = df_ratio.T.mean()
  df_ratio[name]=meanvalue
  # 将该公司名及其指标均值追加到ratio_ind中
  ratio_ind = ratio_ind.append(df_ratio[[name]].T)

## 创建同业评分表和行业标准表 (包含均值、标准差、分位数等)
score_sheet = ratio_ind.T
standard = ratio_ind.describe()

## 遍历每个公司
for i in range(len(ratio_ind)):
  scores = []
  # 遍历每个财务指标
  for j in range(len(ratio_ind.T)):
    # 如果指标值为无穷大，直接给满分
    if np.isinf(ratio_ind.iloc[i,j]) == True:
      n=100
    # 指标值高于75%分位数，得100分
    elif ratio_ind.iloc[i,j]>standard.loc['75%'][j]:
      n = 100
    # 要求4: 判断指标值是否在50%和75%分位数之间
    elif standard.loc['50%'][j]<ratio_ind.iloc[i,j]<=standard.loc['75%'][j]:
      n = 75
    # 指标值在25%和50%分位数之间，得50分
    elif standard.loc['25%'][j]<ratio_ind.iloc[i,j]<=standard.loc['50%'][j]:
      n = 50
    # 否则，得25分
    else:
      n = 25
    scores.append(n)
  # 将得分存入同业评分表
  score_sheet[bj_name[i]]=scores

## 计算每个公司所有指标的同业平均分
ty_score = round(score_sheet.mean(),2)
score_sheet_ty = score_sheet.T
score_sheet_ty['同业评分']=ty_score

10.1.2.4 合并与排名

最后一步，我们将前面计算得到的“趋势评分”和“同业评分”合并到一张总表中，并根据 sec-screening-model 中设定的40/60权重计算综合评分，然后按综合评分进行降序排名，最终得到我们需要的白酒行业上市公司质量排名。

表 10.1

## 要求5: 使用join函数将趋势评分表和同业评分表合并
score_sheet = score_sheet_trend.join(score_sheet_ty)

## 计算综合评分
score_sheet['综合评分']=0.4*score_sheet['趋势评分']+0.6*score_sheet['同业评分']

## 按综合评分降序排列
score_sheet = score_sheet.sort_values(by='综合评分',ascending=False)

## 将结果输出到Excel文件
score_sheet.to_excel('综合评分表.xlsx')

## 在控制台打印关键结果
print("------------------------------------------")
print("2019年各白酒公司排名如下：\n")
## 为了表格美观，这里不直接打印score_sheet，而是创建一个新的DataFrame用于展示
## 实际在notebook环境中，可以直接显示score_sheet[['趋势评分','同业评分','综合评分']]
display_df = score_sheet[['趋势评分','同业评分','综合评分']]

表 10.2: 白酒行业上市公司综合评分排名

display_df

表 tbl-ranking-code 展示了最终的合并、计算与输出代码，其结果在 表 tbl-final-ranking 中呈现。

通过分析 表 tbl-final-ranking 的结果，我们可以清晰地看到基于我们设定的评价框架，哪些白酒公司在2019年表现最为出色。这样的量化排名为投资者提供了非常有价值的参考，帮助他们从众多公司中快速锁定值得进一步深入研究的标的。当然，任何量化模型都是对现实的简化，最终的投资决策还需要结合更多定性因素，如品牌护城河、公司治理、宏观经济政策等进行综合判断。

10.2 基于线性回归模型的财务会计案例实战

同学们好，在前面的课程中，我们学习了如何获取和处理财务数据，以及如何通过财务指标分析来评估一家公司。从本章开始，我们将进入一个全新的领域：利用机器学习模型来挖掘财务数据中更深层次的规律，并进行预测。我们将从最基础也最经典的一元线性回归模型开始，探索变量之间的线性关系。

10.2.1 一元线性回归模型：理论基础

想象一下，你正在研究广告投入与销售额之间的关系。直觉告诉你，广告投得越多，销售额可能就越高。一元线性回归就是将这种“直觉”量化和精确化的统计工具。它旨在寻找一条直线，来最好地拟合（或解释）两个变量之间的关系。

在统计学的语言中，我们试图预测的变量（如销售额）被称为因变量 (Dependent Variable)，我们用来预测的变量（如广告投入）被称为自变量 (Independent Variable)。一元线性回归模型假设这两个变量之间存在线性关系。

10.2.1.1 数学原理

一元线性回归模型可以用一个我们非常熟悉的中学数学公式来表示：

\[ y = ax + b \tag{10.1}\]

在这个模型 (式 eq-sr-model) 中：

• \(y\): 因变量（我们希望预测的值）
• \(x\): 自变量（我们用来预测的输入值）
• \(a\): 回归系数 (Coefficient) 或 斜率 (Slope)，表示 \(x\) 每增加一个单位，\(y\) 平均会发生多大的变化。这是衡量两个变量关系强度的关键。
• \(b\): 截距 (Intercept)，表示当 \(x=0\) 时，\(y\) 的期望值。

模型的目的，就是找到最优的 \(a\) 和 \(b\)，使得这条直线能够最大程度地贴近我们观察到的数据点。那么，如何定义“最好地贴近”呢？

在统计学和机器学习中，最常用的方法是普通最小二乘法 (Ordinary Least Squares, OLS)。它的核心思想是：最优的直线，是那条能让所有数据点的实际值 (\(y_i\)) 与直线上对应的预测值 (\(\hat{y}_i\)) 之间的差值（即残差）的平方和最小的直线。这个残差平方和 (Sum of Squared Residuals, SSR) 公式如下：

\[ SSR = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = \sum_{i=1}^{n} (y_i - (ax_i + b))^2 \tag{10.2}\]

在机器学习领域，这个SSR也被称为损失函数 (Loss Function)。通过微积分的知识，对 式 eq-sr-ssr 分别求关于 \(a\) 和 \(b\) 的偏导数，并令其等于零，就可以解出最优的 \(a\) 和 \(b\)。好在，Python中的科学计算库已经为我们封装好了这个过程，我们无需手动进行复杂的数学推导。

10.2.2 使用 Python 实现一元线性回归

在Python中，实现线性回归最常用的库是scikit-learn，它是一个功能强大且用户友好的机器学习库。让我们通过一个简单的例子来学习基本步骤。

假设我们有以下几组数据点：

• 自变量 X: [1, 2, 4, 5]
• 因变量 Y: [2, 4, 6, 8]

第一步：数据可视化

在建模之前，首先将数据点绘制成散点图是一个好习惯，这可以帮助我们直观地判断是否存在线性关系。

import matplotlib.pyplot as plt

## 注意：为了兼容scikit-learn的输入格式，自变量X通常需要是二维数组的形式
X = [,,,]
Y =

plt.scatter(X, Y)
plt.xlabel('自变量 X')
plt.ylabel('因变量 Y')
plt.grid(True)
plt.show()

图 10.1

从 图 fig-sr-scatter-demo 中可以明显看出，这些点大致分布在一条直线上。

第二步：模型训练与可视化

接下来，我们使用scikit-learn中的LinearRegression对象来构建和训练模型。

from sklearn.linear_model import LinearRegression

## 重新定义数据以确保此代码块独立可运行
X = [,,,]
Y =

## 1. 创建一个线性回归模型对象
regr = LinearRegression()

## 2. 使用fit()方法，传入自变量X和因变量Y来训练模型
regr.fit(X,Y)

## 3. 模型可视化
plt.scatter(X, Y, label='原始数据点')
## 使用regr.predict(X)来获取模型对X的预测值，从而绘制回归线
plt.plot(X, regr.predict(X), color='red', linewidth=2, label='回归线')
plt.xlabel('自变量 X')
plt.ylabel('因变量 Y')
plt.grid(True)
plt.legend()
plt.show()

图 10.2

如 图 fig-sr-fit-demo 所示，scikit-learn已经为我们找到了那条“最优”的直线。

第三步：模型预测与参数查看

模型训练好之后，我们就可以用它来进行预测，并查看其内部参数 \(a\) 和 \(b\)。

列表 10.4

## 重新定义模型和数据
from sklearn.linear_model import LinearRegression
X = [,,,]
Y =
regr = LinearRegression()
regr.fit(X,Y)

## 预测一个新的数据点，例如 x = 3
new_x = []
predicted_y = regr.predict(new_x)
print(f'当 x = {new_x} 时, 模型的预测值 y 为: {predicted_y:.2f}')

## 同时预测多个数据点
multi_new_x = [[1.5], [2.5], [4.5]]
predicted_multi_y = regr.predict(multi_new_x)
print(f'当 x 分别为 {multi_new_x} 时, 预测的 y 值为: {predicted_multi_y}')

## 查看模型的系数a (regr.coef_) 和截距b (regr.intercept_)
print(f'回归系数 a (斜率) 为: {regr.coef_:.2f}')
print(f'截距 b 为: {regr.intercept_:.2f}')
print(f'因此，回归方程为: y = {regr.coef_:.2f} * x + {regr.intercept_:.2f}')

10.2.3 案例分析：茅台线上销量与营业收入的关系

理论学习完毕，让我们进入一个真实的商业场景。随着电商的蓬勃发展，线上销售已成为企业收入的重要来源。我们希望探究一个问题：贵州茅台的线上销量与其季度营业收入之间是否存在线性关系？我们能否通过线上销量来预测其营业收入？

我们将使用贵州茅台2015年至2020年的季度数据进行分析。

10.2.3.1 数据加载与准备

首先，我们加载数据，并将线上销量作为自变量X，营业收入作为因变量Y。为了模拟真实预测场景，我们在此次分析中，将使用大部分历史数据作为训练集(Training Set)来构建模型，并保留最近的四个季度数据作为测试集(Test Set)，用以检验模型的预测效果。

列表 10.5

import pandas as pd
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

## 导入Python中的Scikit-learn机器学习库中的线性回归模型
from sklearn.linear_model import LinearRegression

df = pd.read_excel('一元回归-茅台酒.xlsx')

## 线上销量为自变量，营业收入为因变量
## 我们去掉近四个季度的数据来做训练
X = df[['线上销量']][:-4]
Y = df['营业收入'][:-4]

## 将最后四个季度的数据作为测试数据
Online_data = df[['线上销量']][-4:]

print("训练数据 (X) 的最后几行:")
print(X.tail())
print("\n测试数据 (Online_data) 的内容:")
print(Online_data)

10.2.3.2 模型训练与可视化

我们使用准备好的训练数据来训练线性回归模型，并将其可视化，直观感受线上销量与营业收入的关系。

## 创建一个名为regr的线性回归模型对象
regr = LinearRegression()
## 使用机器学习中的线性回归算法来拟合训练数据集
regr.fit(X,Y)

## 模型可视化
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用于显示中文标签
plt.rcParams['axes.unicode_minus'] = False   # 用来正常显示负号
plt.figure(figsize=(10, 6))
plt.scatter(X,Y, label='训练数据')
plt.plot(X, regr.predict(X), color='red', label='拟合的回归线')
plt.title('贵州茅台线上销量与营业收入关系')
plt.xlabel('线上销量 (X)')
plt.ylabel('营业收入 (Y)')
plt.grid(True)
plt.legend()
plt.show()

## 打印出学习到的线性函数中的系数
print('系数a为:' + str(round(regr.coef_,2)))
print('截距b为:' + str(round(regr.intercept_,2)))

图 10.3

从 图 fig-sr-moutai-fit 中我们可以看到，数据点紧密地分布在回归线周围，表明线上销量和营业收入之间存在着强烈的正向线性关系。根据输出的系数，我们可以写出预测模型：

营业收入 ≈ 10.2 * 线上销量 + 813847

10.2.3.3 模型预测与评估

现在，我们将使用训练好的模型来预测我们预留的最后四个季度（测试集）的营业收入，并与真实值进行比较，以评估模型的预测能力。

## 使用训练好的模型对新的数据集 Online_data 进行预测
P = pd.DataFrame(regr.predict(Online_data))

## 准备绘图用的完整数据序列
Origin_Y = df['营业收入'] # 完整的真实Y值
## 将训练部分的Y值和预测出的测试部分Y值拼接起来
Predict_Y = pd.concat([Y,P],ignore_index=True)

plt.figure(figsize=(12, 7))
plt.plot(Origin_Y.index, Origin_Y, color='red', marker='o', linestyle='--', label='真实营业收入')
plt.plot(Predict_Y.index, Predict_Y, color='blue', marker='x', linestyle='-', label='模型预测营业收入')
plt.title('贵州茅台营业收入：真实值 vs. 预测值')
plt.xlabel('季度索引')
plt.ylabel('营业收入')
## 在图中标出训练集和测试集的分割线
plt.axvline(x=len(Y)-0.5, color='green', linestyle=':', label='训练/测试分割点')
plt.grid(True)
plt.legend()
plt.show()

## 可以看出，预测值与真实值虽然有一定误差，但总体趋势是正确的。

图 10.4

在 图 fig-sr-moutai-predict 中，红线代表了茅台历个季度的真实营业收入，而蓝线代表了我们模型的预测。我们可以看到，在训练集部分（分割线左侧），蓝线与红线几乎重合，这是因为模型本身就是基于这些数据训练的。更关键的是在测试集部分（分割线右侧），模型的预测值（蓝线）虽然与真实值（红线）存在一些误差，但它准确地捕捉到了营业收入持续增长的总体趋势。这初步证明了我们的模型具有一定的预测价值。

在下一章节，我们将学习如何用更精确的统计指标（如R-squared和P值）来量化评估我们模型的好坏。

10.3 线性回归模型评估

上一章我们成功构建了一个预测茅台营业收入的线性回归模型，并通过图形直观地感受了它的预测效果。但是，在严谨的商业分析中，“看起来不错”是远远不够的。我们需要一套量化的、客观的标准来评估模型的性能。本章将介绍评估线性回归模型的“三驾马车”：R-squared、Adjusted R-squared 和 P-value。

10.3.1 模型评估的“三驾马-车”

为了进行更深入的统计评估，我们将引入一个新的Python库：statsmodels。与侧重于预测的scikit-learn不同，statsmodels更侧重于统计推断，它能提供详尽的统计报告，这正是我们评估模型所需要的。

10.3.1.1 R-squared (决定系数, R²)

R-squared 是衡量线性回归模型拟合优度的最常用指标。它的取值范围在0到1之间，数值越接近1，表示模型对数据的解释能力越强。

要理解 R²，我们需要先了解三个“平方和”的概念：

• 整体平方和 (Total Sum of Squares, TSS): 观测值的真实值与其均值之差的平方和。它衡量了因变量 \(Y\) 本身的总变异程度。 \[ TSS = \sum(Y_i - \bar{Y})^2 \]

• 残差平方和 (Residual Sum of Squares, RSS): 观测值的真实值与模型预测值之差的平方和。它衡量了模型未能解释的那部分变异。 \[ RSS = \sum(Y_i - \hat{Y}_i)^2 \]

• R-squared的计算公式 如下： \[ R^2 = 1 - \frac{RSS}{TSS} \tag{10.3}\]

从公式 式 eq-r-squared 可以看出，当模型完美预测时（RSS=0），\(R^2=1\)。当模型预测效果和直接用均值来预测一样差时（RSS=TSS），\(R^2=0\)。因此，\(R^2\)可以被直观地理解为“因变量的总变异中，能够被自变量解释的百分比”。例如，\(R^2=0.92\) 意味着自变量（线上销量）能够解释因变量（营业收入）92%的变异。

10.3.1.2 Adjusted R-squared (调整后决定系数)

一个需要注意的问题是，当我们在模型中增加更多的自变量时（即使是无关的变量），\(R^2\)的值只会上升或保持不变，绝不会下降。这可能会误导我们构建一个过于复杂的模型。

Adjusted R-squared 就是为了解决这个问题而生的。它在 \(R^2\) 的基础上，引入了对模型中自变量个数的“惩罚项”。其公式为：

\[ \text{Adj. } R^2 = 1 - \frac{(1-R^2)(n-1)}{n-k-1} \tag{10.4}\]

其中，\(n\) 是样本数量，\(k\) 是自变量的数量。从公式 式 eq-adj-r-squared 可以看出，每增加一个自变量（\(k\) 增大），分母会变小，从而对整个值施加一个向下的压力。只有当新增的自变量对模型解释力的提升足够大时，Adjusted R² 才会上升。因此，在比较包含不同数量自变量的模型时，Adjusted R² 是一个更公允的评价指标。

10.3.1.3 P-value (P值)

\(R^2\) 告诉我们模型整体拟合得好不好，而 P-value 则是用来判断单个自变量是否真的对因变量有显著影响。

P-value 源于统计学中的假设检验。对于每个自变量的系数（例如模型 \(y = ax+b\) 中的 \(a\)），我们都进行一次检验： - 原假设 (Null Hypothesis, \(H_0\)): 该系数的真实值为0，即该自变量与因变量无关。 - 备择假设 (Alternative Hypothesis, \(H_a\)): 该系数的真实值不为0，即该自变量与因变量有关。

P-value 的含义是：如果原假设为真（即变量真的无关），我们观测到现有数据或更极端数据的概率是多少。 - 如果P-value很小 (通常以0.05为阈值)，说明在“变量无关”的假设下，出现我们当前观测到的强相关数据是极小概率事件。因此，我们有理由拒绝原假设，认为该自变量是显著的。 - 如果P-value很大，说明即使变量真的无关，也很容易观测到现有数据，所以我们没有理由拒绝原假设，认为该自变量是不显著的。

总结一下：P值越小，变量越重要！

10.3.2 案例实战：评估茅台销量预测模型

现在，让我们运用 statsmodels 库来获取茅台销量预测模型的详细评估报告。这次我们将使用全部数据来构建模型，以得到一个更稳健的评估结果。

列表 10.6

import pandas as pd
import statsmodels.api as sm

## 1. 读取全部数据
df = pd.read_excel('一元回归-茅台酒.xlsx')
X = df[['线上销量']]
Y = df['营业收入']

## 2. 添加常数项
## statsmodels默认不包含截距b，需要我们手动添加
X2 = sm.add_constant(X)

## 3. 构建并拟合OLS模型
## OLS是Ordinary Least Squares（普通最小二乘法）的缩写
est = sm.OLS(Y, X2).fit()

## 4. 打印模型的详细评估报告
print("线性回归方程的拟合信息\n")
print(est.summary())

10.3.2.1 解读评估报告

列表 lst-eval-moutai-ols 输出的这张表格信息量巨大，让我们来解读其中最重要的几个值： - R-squared: 0.993。这是一个非常高的值，说明我们的模型（线上销量）可以解释营业收入总变异的99.3%。模型的整体拟合优度极高。 - Adj. R-squared: 0.992。与R-squared非常接近，因为我们只有一个自变量，惩罚项影响很小。 - coef (系数) 下的 线上销量: 10.1517。这就是我们模型中的系数 \(a\)。 - P>|t| (P-value) 下的 线上销量: 0.000。这个值远小于0.05，表明线上销量这个变量对营业收入有极强的统计显著性。我们可以非常有信心地说，线上销量不是一个无关紧要的变量。

综合来看，各项指标都表明，我们构建的一元线性回归模型是一个非常优秀的模型。

10.3.3 模型改进探索：多项式回归

线性模型虽然简单有效，但有时变量间的关系并非严格的直线。可能是一种曲线关系，例如，增长率先快后慢。这时，我们可以通过引入自变量的高次项（如平方项 \(x^2\)）来构建多项式回归模型，以拟合这种曲线关系。

让我们尝试为茅台的模型增加一个“线上销量的平方”项，看看能否进一步提升模型性能。

列表 10.7

import warnings
warnings.filterwarnings("ignore")
from sklearn.preprocessing import PolynomialFeatures

## 1. 创建一个二次多项式特征生成器
poly_reg = PolynomialFeatures(degree=2)

## 2. 使用fit_transform将原始X转换为包含X和X^2的新特征矩阵
X_ = poly_reg.fit_transform(X)

## 3. 为新特征矩阵添加常数项
X2 = sm.add_constant(X_) 

## 4. 拟合新的OLS模型
est = sm.OLS(Y, X2).fit()

## 5. 打印评估报告
print("一元二次回归方程的拟合信息\n")
print(est.summary())

10.3.3.1 比较模型

让我们对比一下 列表 lst-eval-moutai-poly 输出的新报告和之前线性模型的报告： - R-squared 和 Adj. R-squared 都从0.993/0.992微升至 0.993/0.993。提升非常微小。 - 在P>|t|列中，代表 \(x^2\) 的x2变量，其P值为 0.582，远大于0.05。

结论：尽管加入平方项让R²有微乎其微的提升，但该项的P值表明它并不显著。这意味着引入二次项对模型没有实质性的帮助，反而增加了不必要的复杂性。根据奥卡姆剃刀原则（如无必要，勿增实体），我们应该选择更简单的一元线性模型。这个例子也很好地展示了为什么我们不能只看R-squared，而必须结合P-value来综合判断。

10.4 基于多产品的营业收入预测：多元线性回归

在之前的章节中，我们聚焦于研究单个自变量（如线上销量）对因变量（营业收入）的影响。然而，在现实的商业世界中，一个结果往往是多个因素共同作用的结果。例如，一家公司的总收入，并不仅仅来自一种产品，而是其产品矩阵中所有产品销量的总和。这时，我们就需要从一元线性回归升级到多元线性回归（Multiple Linear Regression）。

10.4.1 从“一”到“多”：多元线性回归模型

多元线性回归的原理与一元线性回归一脉相承，都是通过最小二乘法找到一个最佳的拟合模型。其区别在于，模型的方程中包含多个自变量。其通用形式如下：

\[ y = k_0 + k_1x_1 + k_2x_2 + \dots + k_px_p \tag{10.5}\]

在这个模型 (式 eq-mr-model) 中： - \(y\): 依然是我们的因变量。 - \(x_1, x_2, \dots, x_p\): 是 \(p\) 个不同的自变量。 - \(k_0\): 是截距项。 - \(k_1, k_2, \dots, k_p\): 是每个自变量对应的回归系数。\(k_i\) 的含义是：在其他所有自变量保持不变的情况下，\(x_i\) 每增加一个单位，\(y\) 平均会发生 \(k_i\) 个单位的变化。

10.4.2 数据预处理：特征缩放的必要性

在处理多元回归时，一个常见的问题是各个自变量（即“特征”）的量纲 (Scale) 可能完全不同。例如，我们想用“门店数量”（单位：个，数值可能在几十到几千）和“广告投入”（单位：万元，数值可能在几百万到上亿）来预测销售额。如果直接将这些原始数据放入模型，数值范围大的特征（广告投入）可能会在模型中占据主导地位，导致模型对数值范围小的特征（门店数量）不够敏感，从而影响模型的准确性和解释性。

为了解决这个问题，我们需要在建模前对数据进行特征缩放 (Feature Scaling)，将所有特征转换到相似的数值范围内。最常见的两种方法是：

10.4.2.1 Min-Max 标准化

Min-Max 标准化，也称离差标准化，通过一个简单的线性变换将原始数据缩放到 [0, 1] 的区间内。其转换公式为：

\[ x^* = \frac{x - \text{min}(x)}{\text{max}(x) - \text{min}(x)} \tag{10.6}\]

其中，\(x\) 是原始值，\(x^*\) 是转换后的值，\(\text{min}(x)\) 和 \(\text{max}(x)\) 分别是该特征在所有样本中的最小值和最大值。

10.4.2.2 Z-score 标准化

Z-score 标准化，也称均值归一化，它会将原始数据转换为均值为0，标准差为1的标准正态分布。其转换公式为：

\[ x^* = \frac{x - \mu}{\sigma} \tag{10.7}\]

其中，\(\mu\) 是该特征的均值，\(\sigma\) 是该特征的标准差。Z-score标准化后的数据没有固定的范围，但大部分数据会集中在-3到3之间。这种方法对于处理异常值（outliers）相对不那么敏感。

10.4.3 案例分析：海天味业营收预测

与主要依赖单一产品“茅台酒”的贵州茅台不同，像海天味业这样的调味品公司，其营业收入由多种产品共同贡献，例如酱油、蚝油、酱类及其他产品。这是一个应用多元线性回归的绝佳案例。我们将利用海天味业不同品类的线上销量数据来预测其总营业收入。

10.4.3.1 初步建模与评估

我们首先在未经缩放的原始数据上构建模型，并利用 statsmodels 查看其详细的统计报告。

列表 10.8

import pandas as pd
import statsmodels.api as sm
from sklearn.linear_model import LinearRegression

## 导入Python中的sklearn.preprocessing库，并从中引入了MinMaxScaler类
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler

df = pd.read_excel('多元回归-海天味业.xlsx')

X = df[['酱油', '蚝油', '酱类','其他']]
Y = df['营业收入']

## 使用scikit-learn快速查看系数
regr = LinearRegression()
regr.fit(X,Y)
print('各系数为:' + str(regr.coef_.round(2)))
print('常数项系数k0为:' + str(round(regr.intercept_,2)))

## 使用statsmodels获取详细报告
X2 = sm.add_constant(X)
est = sm.OLS(Y, X2).fit()
print("\n多元回归模型详细评估报告:")
print(est.summary())

从 列表 lst-mr-haitian-summary 的报告中，我们可以解读出： - Adj. R-squared: 0.999，模型的整体拟合度极高。 - P>|t| (P值): “酱油”、“蚝油”、“酱类”的P值都为0.000，表明它们都是对营业收入有极显著影响的预测变量。而“其他”这一项的P值为0.781，远大于0.05，说明在其他变量存在的情况下，“其他”类产品的销量对总营收没有显著的独立解释能力。这在商业上是合理的，因为这类产品通常是零散、不成体系的。 - coef (系数): 例如，“酱油”的系数约为2.37，意味着在其他产品销量不变的情况下，酱油销量每增加1个单位，总营业收入预计增加2.37个单位。

10.4.3.2 特征缩放后的模型

虽然初步模型效果很好，但为了养成良好的数据处理习惯，并为将来更复杂的模型做准备，我们仍然演示一下特征缩放的过程。特征缩放后的系数大小可以直接反映不同特征对因变量的影响程度。

列表 10.9

## min-max标准化
## 使用MinMaxScaler类对数据X进行最小-最大缩放
X_new_minmax = MinMaxScaler().fit_transform(X)
regr_minmax = LinearRegression()
regr_minmax.fit(X_new_minmax,Y)
## 将一个线性回归模型(regr)对数据进行了最小-最大值标准化后的系数(coef_)输出
print('min-max标准化后各系数为:' + str(regr_minmax.coef_.round(2)))
print('min-max标准化后常数项系数k0为:' + str(round(regr_minmax.intercept_,2)))
print("-" * 50)

## Z-score标准化
X_new_zscore = StandardScaler().fit_transform(X)
regr_zscore = LinearRegression()
regr_zscore.fit(X_new_zscore,Y)
print('Z-score标准化后各系数为:' + str(regr_zscore.coef_.round(2)))
print('Z-score标准化后常数项系数k0为:' + str(round(regr_zscore.intercept_,2)))

在 列表 lst-mr-haitian-scaled 的结果中，我们可以看到： - 特征缩放后，模型的截距 (intercept_) 发生了显著变化，这是正常的，因为它现在代表所有自变量都取其“缩放后”的0值（对于Min-Max是最小值，对于Z-score是均值）时Y的取值。 - 观察Z-score标准化后的系数 [16578.43, 4443.08, 1261.27, -90.95]。由于所有特征现在都在同一个尺度上（均值为0，标准差为1），我们可以直接比较这些系数的绝对值大小来判断特征的相对重要性。显然，酱油（16578.43）对营收的贡献最大，其次是蚝油（4443.08），再其次是酱类（1261.27），而“其他”的系数很小且为负，进一步印证了它在模型中的不重要性。

这个案例清晰地展示了多元线性回归在分析多因素影响问题上的威力，以及特征缩放对于模型解释性的重要作用。

10.5 财务舞弊识别：决策树模型

到目前为止，我们所学的线性回归模型非常擅长处理变量间存在线性关系的问题。然而，现实世界中的决策过程往往更加复杂，充满了“如果…那么…”的逻辑分支。例如，银行在审批贷款时，会根据申请人的收入、信用记录、负债情况等一系列条件进行判断。这种层层递进的决策逻辑，正是决策树 (Decision Tree) 模型所擅长的。本章，我们将学习如何构建决策树模型来解决一个极具挑战性的商业问题：财务舞弊预测。

10.5.1 决策的艺术：理解决策树

决策树是一种非常直观的机器学习模型，它的结构就像一个流程图。每个内部节点代表对一个特征（或属性）的测试，每个分支代表一个测试输出，而每个叶节点则代表一个类别标签（在分类问题中）或一个数值（在回归问题中）。

让我们用一个经典的员工离职预测例子来理解它：

一个简单的员工离职预测决策树

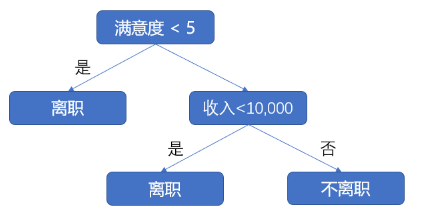
上图的决策逻辑可以翻译为： 1. 首先检查“员工满意度”是否小于5？ 2. 如果是（True），则直接判断该员工会“离职”。 3. 如果否（False），则再检查“收入”是否小于10,000？ 4. 如果是（True），则判断该员工会“离职”。 5. 如果否（False），则判断该员工“不离职”。

这个过程的核心在于，模型通过学习数据，自动找到了最优的“问题”序列（即节点和分裂条件），来最大化决策的准确性。

10.5.1.1 分类决策树：纯度与选择

在分类问题中，决策树的目标是在每个节点进行一次划分，使得划分后的子节点“尽可能纯”。所谓“纯”，指的是子节点内的数据样本尽可能属于同一个类别。衡量“纯度”最常用的两个指标是基尼不纯度 (Gini Impurity) 和信息熵 (Information Entropy)。

• 基尼不纯度：计算的是从一个节点中随机抽取两个样本，其类别标签不一致的概率。基尼不纯度越低，节点的纯度越高。一个完全纯的节点（所有样本都属于同一类）基尼不纯度为0。 \[ \text{Gini}(T) = 1 - \sum_{i=1}^{c} (p_i)^2 \]

  其中 \(p_i\) 是类别 \(i\) 在节点 \(T\) 中的样本比例。决策树在分裂时，会选择那个能让分裂后子节点的加权基尼不纯度总和最小的特征和分裂点。这个算法被称为CART (Classification and Regression Tree)。

• 信息熵：源于信息论，衡量的是一个系统的不确定性或“混乱程度”。信息熵越低，系统越有序，纯度越高。决策树通过计算分裂前后的信息增益 (Information Gain)（即熵的减少量），选择信息增益最大的分裂方式。

在scikit-learn中，DecisionTreeClassifier默认使用基尼不纯度作为分裂标准。

10.5.1.2 回归决策树：最小化误差

当因变量是连续数值时（如预测股价、房价），决策树也可以用来做回归。回归决策树的分裂标准不再是“纯度”，而是均方误差 (Mean Squared Error, MSE)。 \[ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \bar{y})^2 \]

其中，\(y_i\)是节点内每个样本的真实值，\(\bar{y}\)是该节点所有样本真实值的平均值。决策树会选择能使分裂后两个子节点的加权MSE总和最小的分割点。最终，落在同一个叶子节点的所有样本，其预测值都将是该叶子节点所有训练样本的平均值。

10.5.2 案例分析：构建财务舞弊预测模型

财务舞弊是资本市场的“毒瘤”，给投资者带来巨大损失。如果能构建一个模型，提前识别出具有舞弊风险的公司，将具有重大的实用价值。这是一个典型的二分类问题：一家公司“舞弊”或“不舞弊”。

我们将使用一个包含中国上市公司2010-2019年财务数据、市场数据和宏观经济数据的真实数据集。其中，是否舞弊的标签（1代表舞弊，0代表正常）是根据公开的处罚公告整理的。

10.5.2.1 数据探索与预处理

真实世界的数据往往是不完美的，充满缺失值和异常值。在建模前，必须进行细致的预处理。

列表 10.10

import pandas as pd
import numpy as np
from collections import Counter

fraud_data = pd.read_excel('财务数据2010_2019.xlsx')

## 查看数据中舞弊与非舞弊公司的数量
print("原始数据中各类别的数量:")
print(fraud_data['是否舞弊'].value_counts())
print("\n原始数据中各列的缺失值数量:")
print(fraud_data.isnull().sum().to_frame('缺失数量').T)

## 打印并删除缺失值比例大于50%的列
for t in fraud_data.columns:
    if fraud_data[t].isnull().sum()/len(fraud_data)>0.5:
        print(f"列 '{t}' 缺失率超过50%，予以删除。")
        fraud_data = fraud_data.drop(columns=t)

## 缺失数据用中位数填充
fraud_data = fraud_data.fillna(fraud_data.median())

## 无穷大(inf)处理, 先替换为NaN，再用该列的最大值填充
fraud_data[np.isinf(fraud_data)] = np.nan
fraud_data = fraud_data.fillna(fraud_data.max())

print("\n处理后数据中是否还有缺失值:")
print(fraud_data.isnull().sum().to_frame('缺失数量').T)

从 列表 lst-dt-data-prep 的输出可以看到，这是一个典型的不平衡数据集 (Imbalanced Dataset)：正常公司的样本数量远多于舞弊公司。这会给模型训练带来麻烦，我们稍后处理。

10.5.2.2 应对不平衡数据：SMOTE过采样技术

如果直接用不平衡数据训练模型，模型很可能会“偷懒”，简单地将所有公司都预测为“正常”，也能获得很高的准确率（Accuracy），但这显然不是我们想要的。我们需要模型能够准确地“揪出”那些少数的舞弊公司。

SMOTE (Synthetic Minority Over-sampling Technique) 是一种强大的过采样技术，专门用来解决数据不平衡问题。它的基本思想是：对于少数类（舞弊公司）的每一个样本，从其最近的k个同类样本中随机选择一个，然后在这两个样本的连线上随机取一点，生成一个新的、人工合成的少数类样本。通过这种方式，可以在不直接复制原始数据的情况下，增加少数类的样本数量，使数据集变得平衡。

列表 10.11

from imblearn.over_sampling import SMOTE
from sklearn.model_selection import train_test_split # 虽然PPT是按年份，但随机划分更常用

## 为了演示，我们先按年份划分训练集和测试集
train_year = [i for i in range(2009,2018)]
test_year =

train = fraud_data[fraud_data["年份"].isin(train_year)]
test = fraud_data[fraud_data["年份"].isin(test_year)]

## 提取特征变量(X)和目标变量(y)
X_train = train.drop(columns=['索引', '年份', '是否舞弊'])
y_train = train['是否舞弊']
X_test = test.drop(columns=['索引', '年份', '是否舞弊'])
y_test = test['是否舞弊']


print('原始训练集中y的类别和个数:')
print(Counter(y_train))

## 建立SMOTE模型对象
model_smote = SMOTE(random_state=123)
## 输入数据并进行过采样处理
X_smote_resampled, y_smote_resampled = model_smote.fit_resample(X_train, y_train)

print('\n经过SMOTE处理后训练集中y的类别和个数:')
print(Counter(y_smote_resampled))

如 列表 lst-dt-smote 所示，经过SMOTE处理后，训练集中的舞弊样本和正常样本数量已经完全相等，数据变得平衡了。

10.5.2.3 模型训练与评估

现在，我们可以使用平衡后的训练数据来训练我们的决策树分类器了。为了防止模型过于复杂导致过拟合 (Overfitting)，我们通过 max_depth 参数限制树的最大深度为3。

from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, roc_auc_score, roc_curve
import matplotlib.pyplot as plt

## 定义一个决策树分类器
model = DecisionTreeClassifier(max_depth=3, random_state=123)
## 使用过采样后的训练数据集进行训练
model.fit(X_smote_resampled, y_smote_resampled)

## 1. 直接预测是否舞弊
y_pred = model.predict(X_test)
print(f"模型在测试集上的准确率为: {accuracy_score(y_test, y_pred):.4f}")

## 2. 预测不舞弊与舞弊的概率
## predict_proba返回一个数组，第一列是不舞弊(0)的概率，第二列是舞弊(1)的概率
y_pred_proba = model.predict_proba(X_test)[:, 1]

## 3. 计算AUC分数
auc = roc_auc_score(y_test, y_pred_proba)
print(f"模型在测试集上的AUC分数为: {auc:.4f}")

## 4. 绘制ROC曲线
fpr, tpr, thres = roc_curve(y_test, y_pred_proba)
plt.plot(fpr, tpr, label=f'Decision Tree (AUC = {auc:.2f})')
plt.plot(,, 'r--', label='Random Guess')
plt.xlabel('假警报率 (False Positive Rate)')
plt.ylabel('命中率 (True Positive Rate)')
plt.title('ROC曲线')
plt.legend()
plt.grid(True)
plt.show()

图 10.5

对于不平衡分类问题，准确率 (Accuracy) 往往不是一个好的评估指标。我们更关心ROC曲线和其曲线下面积AUC (Area Under the Curve)。 - ROC曲线：横坐标是“假警报率”（把正常公司误报为舞弊的比例），纵坐标是“命中率”（正确识别出舞弊公司的比例）。一个优秀的模型，其ROC曲线会尽可能地向左上角靠近，意味着在保持较低误报率的同时，能有较高的命中率。 - AUC值：是ROC曲线下的面积，取值在0.5到1之间。AUC=0.5代表模型毫无分辨能力（相当于随机猜测），AUC=1代表完美分类。我们的模型AUC达到了0.7左右（具体数值每次运行可能稍有不同），说明模型具有一定的舞弊识别能力。

10.5.2.4 解读模型：特征重要性

决策树模型的一大优点是其可解释性。我们可以轻易地知道模型在决策时最看重哪些特征。

表 10.3: 财务舞弊预测模型中最重要的五个特征

## 获取特征重要性
importances = model.feature_importances_
features = X_train.columns

## 通过二维表格形式显示
importances_df = pd.DataFrame()
importances_df['特征名称'] = features
importances_df['特征重要性'] = model.feature_importances_

## 按重要性降序排序并显示前5个
importances_df = importances_df.sort_values('特征重要性', ascending=False)
print(importances_df.head())

从 表 tbl-dt-importance 的结果中，我们可以看到模型认为哪些财务指标对于识别舞弊最为关键。例如，如果“资产减值损失”或“营业收入增长率”等指标排在前面，这可能为审计人员和监管机构提供了非常有价值的线索，指导他们应该重点关注哪些领域。

10.6 财务舞弊预测进阶：集成学习与随机森林

在上一章，我们成功构建了一个决策树模型来预测财务舞弊，并学习了如何处理不平衡数据和评估分类模型。然而，单个决策树模型虽然直观，但有时会因为数据的微小变动而产生巨大差异，稳定性较差，也容易过拟合。为了构建一个更强大、更稳健的预测模型，我们将引入集成学习 (Ensemble Learning) 的思想，并学习其中最具代表性的算法之一：随机森林 (Random Forest)。

10.6.1 集思广益：集成学习的力量

集成学习的核心思想非常符合我们的日常直觉：“三个臭皮匠，顶个诸葛亮”。它不是依赖于单个“天才”模型，而是将多个相对较弱的模型（称为“基学习器”）结合起来，通过集体智慧做出最终决策。

Bagging (Bootstrap Aggregating) 是集成学习的主要方法之一。它的工作流程如下： 1. 自助采样 (Bootstrap): 从原始训练数据集中，有放回地随机抽取 \(n\) 个样本（\(n\) 等于原始数据集的大小），形成一个新的训练子集。重复这个过程 \(m\) 次，我们就得到了 \(m\) 个不同的训练子集。 2. 独立训练 (Aggregating): 使用这 \(m\) 个训练子集，独立地训练出 \(m\) 个基学习器。 3. 集体决策: 对于一个新的预测任务，让这 \(m\) 个模型分别进行预测，然后通过“投票”（分类问题）或“取平均”（回归问题）的方式，得出最终的集成预测结果。

Bagging通过在略有不同的数据子集上训练模型，有效地降低了模型的方差，使其更加稳定和鲁棒。

10.6.2 随机森林：不止是树木的集合

随机森林就是一种基于Bagging思想的、专门以决策树为基学习器的集成模型。但它在Bagging的基础上，又增加了一层“随机性”，使其性能进一步提升。

随机森林模型结构示意图

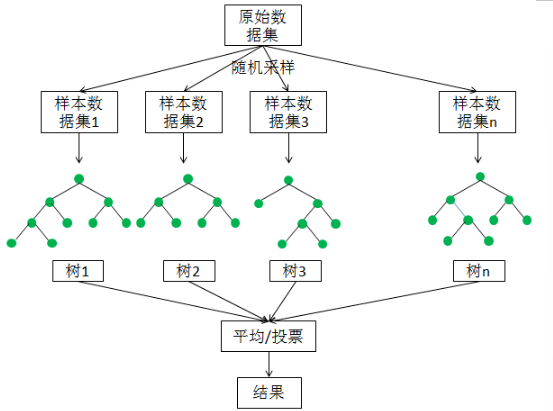
随机森林的两大核心“随机”原则是： 1. 数据随机 (行抽样): 这就是Bagging的自助采样过程。每棵树都在一个不同的数据子集上训练，保证了树之间的“多样性”。 2. 特征随机 (列抽样): 这是随机森林对Bagging的关键改进。在构建每棵决策树的每个节点时，并不是从所有特征中选择最优分裂点，而是先随机抽取一个特征子集，然后再从这个子集中选择最优分裂点。

这种“特征随机”的设计，进一步增强了模型中各个决策树的差异性。它避免了模型过度依赖某些强特征，使得一些弱特征也有机会参与决策过程，从而让整个森林的模型泛化能力更强，更不容易过拟合。

10.6.3 案例再战：使用随机森林提升舞弊预测能力

现在，让我们再次挑战财务舞弊预测任务，这次我们将使用scikit-learn中的RandomForestClassifier，并引入超参数调优技术，力求获得最佳的模型性能。

10.6.3.1 数据准备与模型初建

数据预处理的步骤与上一章类似。但这次我们使用train_test_split进行随机划分，这是机器学习中更通用的做法。然后，我们先构建一个使用默认参数的随机森林模型，看看它的基准性能如何。

列表 10.12

import pandas as pd
import numpy as np
from imblearn.over_sampling import SMOTE
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, roc_auc_score
from sklearn.model_selection import train_test_split

## 1. 读取数据与简单预处理 (与上一章相同)
fraud_data = pd.read_excel('财务数据2010_2019.xlsx')
for t in fraud_data.columns:
    if fraud_data[t].isnull().sum()/len(fraud_data)>0.5:
        fraud_data = fraud_data.drop(columns=t)
fraud_data = fraud_data.fillna(fraud_data.median())
fraud_data[np.isinf(fraud_data)] = np.nan
fraud_data = fraud_data.fillna(fraud_data.max())

## 2. 提取特征和目标变量
X = fraud_data.drop(columns=['索引', '年份', '是否舞弊'])
y = fraud_data['是否舞弊']
## 将数据集X和标签y分成训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)

## 3. 过采样 (仅对训练集)
model_smote = SMOTE(random_state=123)
X_smote_resampled, y_smote_resampled = model_smote.fit_resample(X_train, y_train)

## 4. 创建一个随机森林分类器模型
model = RandomForestClassifier(n_estimators=20, random_state=123)
model.fit(X_smote_resampled, y_smote_resampled)

## 5. 评估模型
y_pred_proba = model.predict_proba(X_test)[:, 1]
auc_score = roc_auc_score(y_test, y_pred_proba)
print(f"基准随机森林模型的AUC值: {auc_score:.4f}")

10.6.3.2 模型调优：网格搜索寻找最优参数

随机森林模型有许多可以调整的超参数 (Hyperparameters)，例如： - n_estimators: 森林中决策树的数量。 - max_depth: 每棵树的最大深度。 - criterion: 节点分裂的标准（‘gini’ 或 ‘entropy’）。

手动去尝试这些参数的不同组合费时费力。scikit-learn提供了一个强大的工具——GridSearchCV (网格搜索与交叉验证)，它可以自动化地替我们找到最优的超参数组合。

它的工作原理是： 1. 我们定义一个“网格”，即我们希望尝试的超参数及其候选值。 2. GridSearchCV 会遍历这个网格中所有可能的参数组合。 3. 对于每一种组合，它使用交叉验证 (Cross-Validation) 的方法来评估模型性能。例如，5折交叉验证会将训练数据分成5份，轮流用4份训练、1份验证，重复5次后取平均分，这样做出的评估更稳健。 4. 最后，它会告诉我们哪种参数组合在交叉验证中表现最好。

列表 10.13

from sklearn.model_selection import GridSearchCV

## 定义要搜索的参数网格
parameters = {
    'n_estimators':, 
    'max_depth':, 
    'criterion': ['gini', 'entropy']
}

## 创建一个新的、不带参数的随机森林模型实例
model = RandomForestClassifier(random_state=123) 

## 设置网格搜索
## scoring='roc_auc' 指定评估指标为AUC
## cv=5 指定使用5折交叉验证
grid_search = GridSearchCV(model, parameters, scoring='roc_auc', cv=5)

## 在过采样后的训练数据上执行搜索
grid_search.fit(X_smote_resampled, y_smote_resampled)

## 打印最优参数组合
print("网格搜索找到的最优参数:", grid_search.best_params_)

## 使用找到的最佳模型进行预测
y_pred_proba = grid_search.predict_proba(X_test)[:, 1]
tuned_auc_score = roc_auc_score(y_test, y_pred_proba)

print(f"调优后模型的准确度: {accuracy_score(y_test, grid_search.predict(X_test)):.4f}")
print(f"调优后模型的AUC: {tuned_auc_score:.4f}")

通过对比 列表 lst-rf-baseline 和 列表 lst-rf-gridsearch-code 的结果，我们可以看到，经过GridSearchCV调优后的随机森林模型，其AUC分数通常会比使用默认参数的模型有所提升。这证明了超参数调优在提升模型性能方面的重要性。更重要的是，相比于上一章的单一决策树模型，随机森林模型通常能达到更高的性能上限和更好的稳定性，是解决类似财务舞弊预测这类复杂分类问题的有力武器。