“在金融工程的广阔天地中，数据是矿石，Python 是炼金术，而数学则是点石成金的咒语。”——课程引言
本章将带领各位大二同学跨入金融科技的大门。作为长三角地区的未来金融从业者,掌握Python这一工具,不仅是为了应对课程作业,更是为了在上海、杭州、南京等金融中心的量化交易、风险管理、金融分析岗位上立足。
我们将从最基础的Python语法开始,迅速过渡到金融数据的获取与处理。不同于计算机专业的Python课程,我们这里的每一个例子、每一行代码,都有着鲜明的金融烙印。
Python语言由荷兰程序员Guido van Rossum于1991年首次发布(Rossum 1995),最初设计目标是提供一种简洁、易读的编程语言。然而,Python真正在金融领域崭露头角始于2000年代中期,这与几个关键发展密不可分:
NumPy的诞生 (2006): Travis Oliphant整合了Numeric和Numarray两个项目,创建了现代NumPy(Oliphant 2006)。NumPy提供的高效数组运算能力使Python首次具备了与MATLAB竞争的能力。
Pandas的革命 (2008): Wes McKinney在对冲基金AQR Capital工作期间,因不满现有工具的局限性,创建了Pandas库(McKinney 2010)。Pandas的DataFrame数据结构完美契合了金融时间序列的处理需求,成为量化金融的基石。
机器学习生态的繁荣 (2010s): Scikit-learn(Pedregosa 等 2011)、TensorFlow(Abadi 等 2016)和PyTorch(Paszke 等 2019)等机器学习框架的出现,使Python成为人工智能在金融领域应用的首选语言。
最新发展: 近年来,Python在量化金融领域的发展呈现以下趋势:
学术参考文献
关于Python在科学计算中的应用,建议阅读以下经典文献:
VanderPlas, J. (2016). Python Data Science Handbook. O’Reilly Media. URL: https://jakevdp.github.io/PythonDataScienceHandbook/
McKinney, W. (2017). Python for Data Analysis. O’Reilly Media. DOI: https://doi.org/10.5555/3203489
Hilpisch, Y. (2018). Python for Finance: Mastering Data-Driven Finance. O’Reilly Media. DOI: https://doi.org/10.5555/3241316
对于金融时间序列分析的理论基础,推荐:
在过去的十年里,Python已经取代了C++和MATLAB,成为金融工程领域的”通用语言”。这得益于其丰富的数据科学生态系统。
推导:Python列表 vs NumPy数组的性能差异
考虑计算两个长度为\(n\)的向量的点积: \[\mathbf{a} \cdot \mathbf{b} = \sum_{i=1}^{n} a_i b_i\]
Python原生列表实现:
result = sum([a[i] * b[i] for i in range(n)])时间复杂度分析: - 每次索引操作: \(O(1)\) - 乘法运算: \(O(1)\) - 加法运算: \(O(1)\) - 总复杂度: \(O(n)\),但常数因子大,因为: 1. Python列表元素是指针,需要间接寻址 2. 每个数字是PyObject,包含类型信息开销 3. 解释器逐行执行,无法矢量化
NumPy数组实现:
result = np.dot(a, b)时间复杂度同为\(O(n)\),但: - 数据连续存储,利用CPU缓存 - 底层调用BLAS(Basic Linear Algebra Subprograms)库 - SIMD(Single Instruction Multiple Data)指令并行计算 - 实测加速比: 对于\(n=10^6\),NumPy比纯Python快50-100倍
金融应用: 在计算投资组合协方差矩阵时,若有1000只股票、252个交易日数据,涉及\((1000 \times 252) \times (1000 \times 252)\)规模的矩阵运算,NumPy的性能优势决定了策略的可行性。
如图 图 1.1 所示,我们处于一个层层递进的生态中。不管是处理宁波港的股价,还是分析宁波银行的财报,我们都离不开这些核心库。
向量化、广播与 dtype：为什么同样是 \(O(n)\)，跑起来差很多
初学者经常把‘复杂度’等同于‘速度’：看到 Python 列表与 NumPy 都是 \(O(n)\) 就以为它们一样快。实际上，差异往往来自 常数项，而常数项背后就是三件事：
float64），内存连续；Python 列表里每个元素是对象指针，访存和类型检查开销更大。在金融里，这些差异会直接决定某些任务是否‘做得动’：例如滚动波动率、协方差矩阵、回测中大量逐日更新的特征。
在金融中,我们需要处理各种类型的数据:股票代码是字符串,价格是浮点数,交易量是整数。Python的动态类型系统简化了代码编写,但也要求我们理解底层数据表示。
浮点数精度问题
金融计算中必须警惕浮点数的精度陷阱。Python使用IEEE 754双精度浮点数(64位),其中: - 1位符号位 - 11位指数位 - 52位尾数位
这导致精度约为\(2.22 \times 10^{-16}\)。例如:
>>> 0.1 + 0.2 == 0.3
False # 因为0.1和0.2无法精确表示为二进制
>>> 0.1 + 0.2
0.30000000000000004金融解决方案: 对于涉及货币的计算,使用decimal模块:
from decimal import Decimal, getcontext
getcontext().prec = 10 # 设置10位精度
price = Decimal('7.24')
shares = Decimal('10000')
total = price * shares # 精确计算# 宁波银行 (002142.SZ) - 浙江地区城商行代表
stock_name = '宁波银行' # String
stock_code = '002142.SZ' # String
current_price = 19.58 # Float (示例价格)
volume = 8530000 # Integer (日均成交量)
is_tradable = True # Boolean
print(f'股票: {stock_name} ({stock_code})')
print(f'当前价格: {current_price}元, 日成交量: {volume:,}股')
print(f'市值估算: {current_price * 1e9:.2e}元 (假设10亿股本)')股票: 宁波银行 (002142.SZ)
当前价格: 19.58元, 日成交量: 8,530,000股
市值估算: 1.96e+10元 (假设10亿股本)投资组合（Portfolio）本质上就是一种容器。
# 长三角上市公司代表
# 600000.SH: 浦发银行 (上海)
# 600276.SH: 恒瑞医药 (江苏连云港)
# 002142.SZ: 宁波银行 (浙江宁波)
yrd_portfolio_list = ['600000.SH', '600276.SH', '002142.SZ']
# 股票与持仓数量的映射
portfolio_position = {
'600000.SH': 10000,
'600276.SH': 500,
'002142.SZ': 2000
}
key_hr = '600276.SH'
print(f'投资组合代码: {yrd_portfolio_list}')
print(f'恒瑞医药持仓: {portfolio_position[key_hr]} 股')投资组合代码: ['600000.SH', '600276.SH', '002142.SZ']
恒瑞医药持仓: 500 股可变对象、浅拷贝与回测‘无意改历史’的坑
在回测/特征工程里，一个典型陷阱是：你以为在修改‘当前持仓’，结果其实把历史记录也改掉了。根因是 列表、字典、DataFrame 这类对象是可变的，而 = 只是引用绑定。
a = b：a 和 b 指向同一个对象。dict.copy() / list.copy()：通常是浅拷贝（只复制最外层容器）。如果你的对象里还嵌套了列表/字典（例如 positions[date][stock] 这样的结构），浅拷贝仍可能导致‘改当前影响历史’。在策略代码里，建议用更明确的方式：
copy.deepcopy()（代价是更慢）这类问题不会报错，但会让回测结果看起来‘太好’，本质上属于一种隐蔽的数据泄露。
Python原生的列表在处理大规模金融时间序列时效率较低，因此我们引入NumPy和Pandas。
NumPy (Numerical Python) 是所有科学计算的基础。下面我们直接使用本项目的本地数据快照中的真实股价数据，演示如何计算对数收益率。
\[ r_t = \ln(\frac{P_t}{P_{t-1}}) \]
import numpy as np
import pandas as pd
from pathlib import Path
df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))
df = (df_all[df_all['ts_code'].eq('002142.SZ')].sort_values('trade_date').dropna(subset=['adj_close']).copy())
prices = df['adj_close'].tail(6).to_numpy(dtype=float)
# 使用 NumPy 计算对数收益率：r_t = ln(P_t) - ln(P_{t-1})
log_returns = np.diff(np.log(prices))
print('宁波银行(002142.SZ)后复权收盘价(最近6个交易日):', np.round(prices, 4))
print('对数收益率(最近5个交易日):', np.round(log_returns, 6))宁波银行(002142.SZ)后复权收盘价(最近6个交易日): [19.58 19.68 19.44 19.48 20.2 20.11]
对数收益率(最近5个交易日): [ 0.005094 -0.01227 0.002055 0.036294 -0.004465]Pandas 提供了 DataFrame（数据框）结构，非常适合处理 OHLC（Open, High, Low, Close）数据。
import pandas as pd
from pathlib import Path
df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))
df_nb = (df_all[df_all['ts_code'].eq('601018.SH')]
.sort_values('trade_date')
.set_index('trade_date')
[['open','high','low','close','volume','amount','adj_close','log_ret']].copy())
print(df_nb.head(5)) open high low close volume amount adj_close \
trade_date
2018-01-02 5.31 5.35 5.29 5.34 120577.99 64226.444 4.702933
2018-01-03 5.34 5.43 5.33 5.40 169253.61 91416.531 4.755775
2018-01-04 5.45 5.49 5.39 5.48 258878.31 140895.447 4.826231
2018-01-05 5.48 5.48 5.41 5.44 157143.95 85480.594 4.791003
2018-01-08 5.43 5.49 5.40 5.46 146356.50 79795.023 4.808617
log_ret
trade_date
2018-01-02 NaN
2018-01-03 0.011173
2018-01-04 0.014706
2018-01-05 -0.007326
2018-01-08 0.003670 作为金融工程师，必须学会从专业数据源获取数据。为了保证教材内容在离线环境中也能稳定复现，本书采用“数据获取与数据分析解耦”的工程做法：
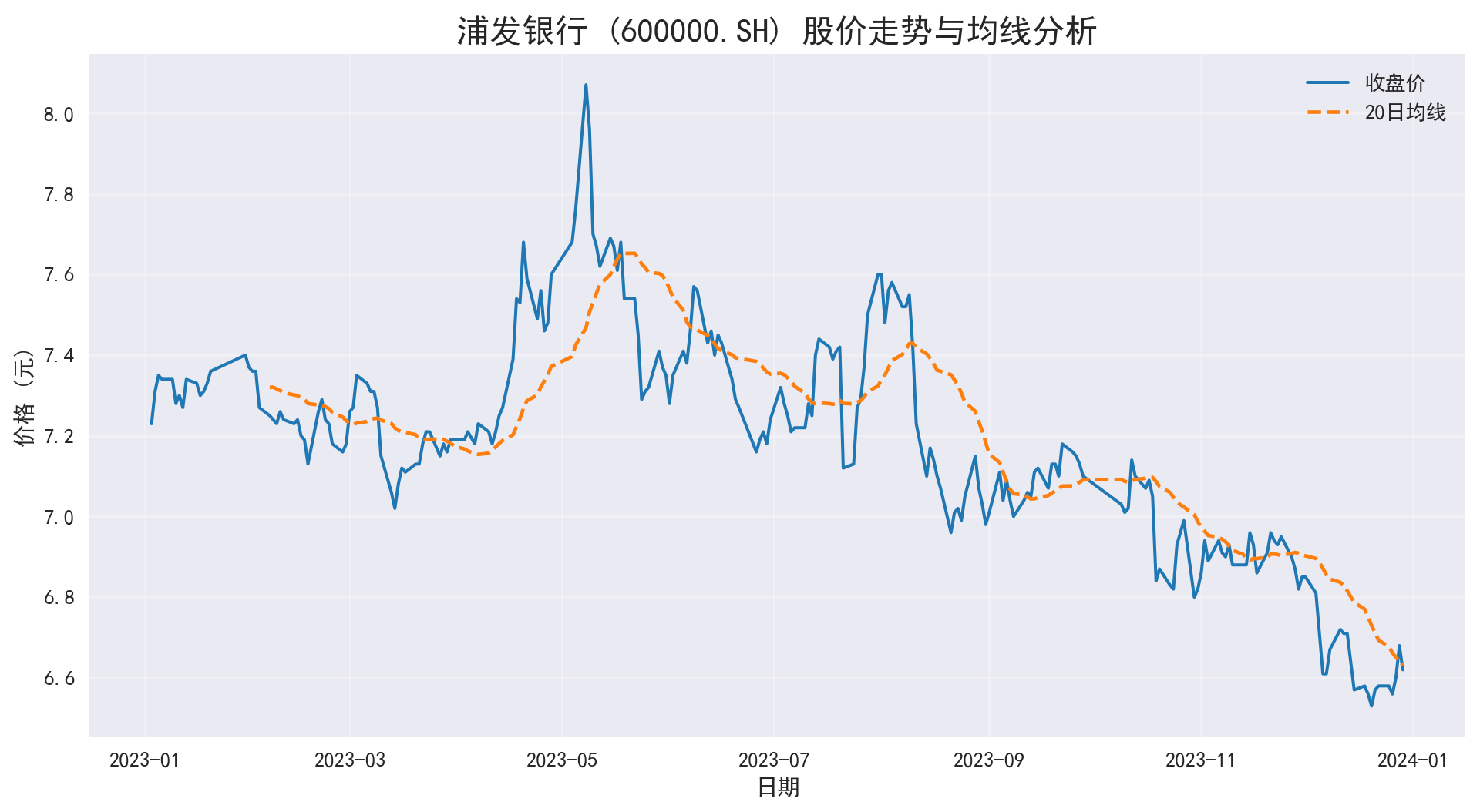
scripts/fetch_cn_market_data.py 负责从数据源拉取，并将原始数据保存到 data/ 目录。data/cn_equity_daily_latest.parquet 这类 *latest.parquet 快照文件，不在文档中直连网络 API。案例对象：浦发银行 (600000.SH)。作为总部位于上海陆家嘴的全国性股份制商业银行，它是长三角金融业发展的缩影。
我们将获取浦发银行 2023 年至今的日线行情数据。
import pandas as pd
from pathlib import Path
df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))
# 案例：浦发银行(600000.SH) 2023 年日线数据（来自本地快照，避免在正文中直连 API）
df_spf = (df_all[df_all['ts_code'].eq('600000.SH')]
.sort_values('trade_date')
.set_index('trade_date')
.loc['2023-01-01':'2023-12-31']
.copy())
print(df_spf[['open','high','low','close','volume','amount']].head()) open high low close volume amount
trade_date
2023-01-03 7.27 7.28 7.17 7.23 258925.21 187094.064
2023-01-04 7.27 7.35 7.23 7.31 309470.81 226321.372
2023-01-05 7.37 7.38 7.30 7.35 301621.54 221617.355
2023-01-06 7.35 7.38 7.31 7.34 203128.81 149170.538
2023-01-09 7.38 7.38 7.30 7.34 196122.60 143998.211获取数据后，最直观的分析方法就是绘图。我们将绘制股价走势图。
我们将配置 Matplotlib 以支持中文字体显示（使用思源宋体 Source Han Serif SC）。
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
# 设置绘图风格
plt.style.use('seaborn-v0_8')
# 配置中文字体：优先使用思源宋体（若系统未安装则自动回退到其他字体）
plt.rcParams['font.family'] = ['Source Han Serif SC', 'SimHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
plt.figure(figsize=(12, 6))
# 绘制收盘价
plt.plot(df_spf.index, df_spf['close'], label='收盘价', color='#1f77b4', linewidth=1.5)
# 添加移动平均线 (Simple Moving Average)
df_spf['MA20'] = df_spf['close'].rolling(window=20).mean()
plt.plot(df_spf.index, df_spf['MA20'], label='20日均线', color='#ff7f0e', linestyle='--')
plt.title('浦发银行 (600000.SH) 股价走势与均线分析', fontsize=16)
plt.xlabel('日期')
plt.ylabel('价格 (元)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
rolling/shift 的“时间对齐”是量化入门最容易忽略的细节
当你写出 rolling(20).mean() 或 shift(1) 时，你其实是在回答一个关键问题：信号在什么时候可得？交易在什么时候发生？
rolling(20).mean() 默认只使用“当日及之前”的窗口，因此它本身通常不会引入未来信息。signal = signal.shift(1)。与本书后续章节对应：第5章回测会反复用到 shift(1) 来确保交易逻辑成立；第6章机器学习也会强调训练/测试必须按时间切分。
本章我们建立起了金融工程的数据地基:
在接下来的章节中,我们将深入探索如何利用这些数据进行风险度量、投资组合优化以及量化策略的构建。
题目1: 数据获取 - 从本项目的本地快照 data/cn_equity_daily_latest.parquet 中提取恒瑞医药 (600276.SH)过去一年的日线数据
题目2: 统计计算 - 利用Pandas计算该股票的日收益率,并求出其标准差(波动率)
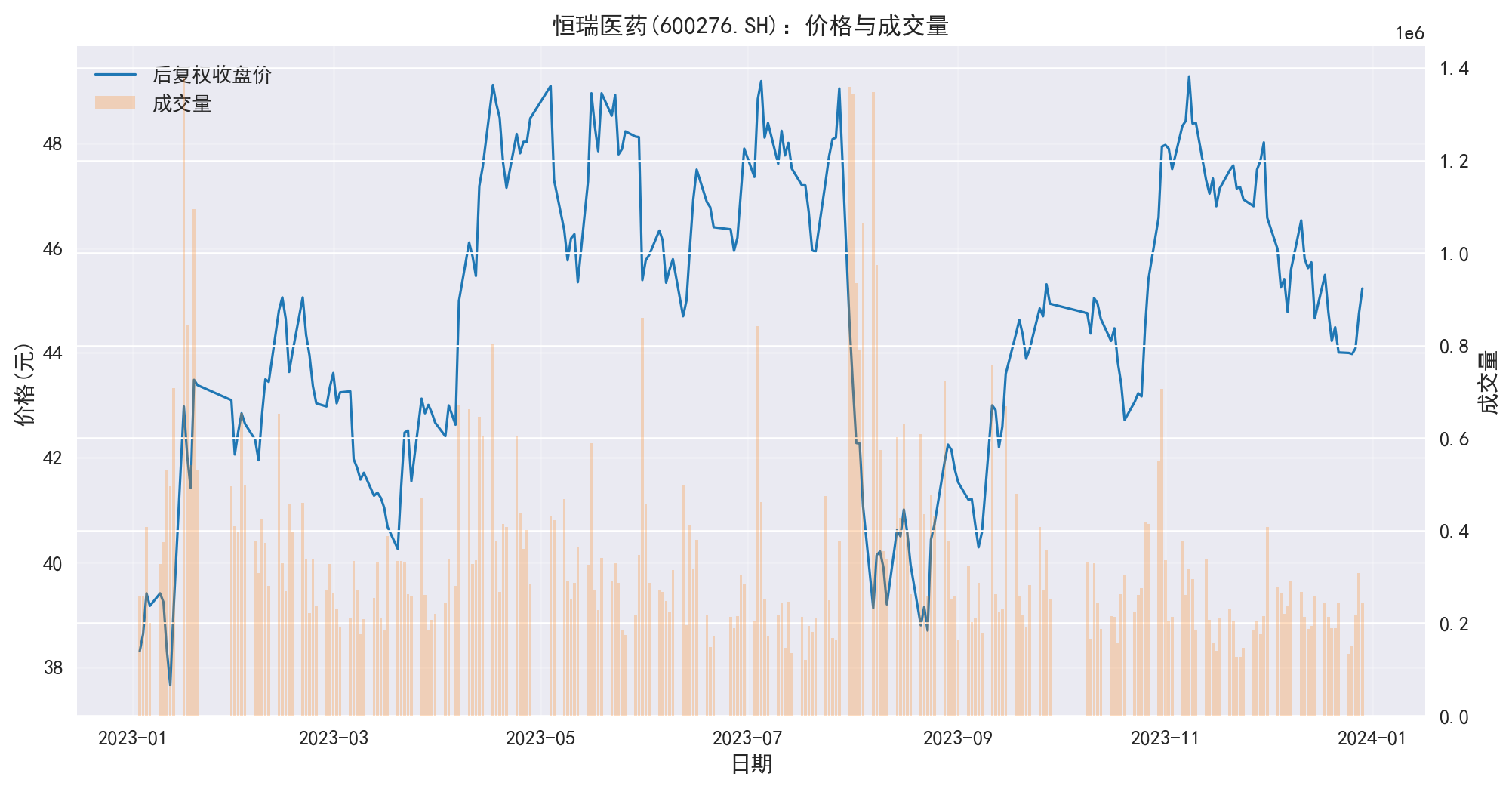
题目3: 可视化 - 绘制收盘价与成交量(Volume)的双轴图
本节给出三道练习题的完整解答。为保证可复现性，所有数据均从本项目 data/ 目录的本地快照读取（不在文档中调用网络 API）。
我们需要从本地面板数据中过滤出目标股票，并按交易日升序排列。
import pandas as pd
from pathlib import Path
df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))
df_hengrui = (df_all[df_all['ts_code'].eq('600276.SH')]
.sort_values('trade_date')
.set_index('trade_date')
.copy())
print(df_hengrui[['open','high','low','close','volume','amount']].tail(5)) open high low close volume amount
trade_date
2023-12-25 44.01 44.55 43.90 44.00 133611.50 590059.431
2023-12-26 44.00 44.07 43.30 43.98 150553.93 657505.418
2023-12-27 43.90 44.21 43.36 44.09 216014.90 947551.025
2023-12-28 44.10 44.85 43.93 44.75 307634.47 1370257.485
2023-12-29 44.88 45.40 44.65 45.23 242380.46 1094134.425常用的两种收益率定义：
在日频数据下，若用样本标准差 \(\sigma_{\text{daily}}\) 估计波动率，常见的年化近似为：
\[ \sigma_{\text{ann}} \approx \sqrt{252}\,\sigma_{\text{daily}} \]
其中 252 是中国 A 股一年中大致的交易日数量（在不同年份略有差异，但作为近似足够）。
import numpy as np
# 使用后复权收盘价计算收益率（更适合跨期比较）
px = df_hengrui['adj_close'].dropna()
ret_simple = px.pct_change().dropna()
ret_log = np.log(px / px.shift(1)).dropna()
vol_daily = ret_log.std(ddof=1)
vol_annual = np.sqrt(252) * vol_daily
print(f'日对数收益率波动率(样本): {vol_daily:.6f}')
print(f'年化波动率(近似): {vol_annual:.2%}')日对数收益率波动率(样本): 0.022348
年化波动率(近似): 35.48%量价图常用于技术分析：价格反映市场预期，成交量反映交易热度与流动性。双轴图能把两者放在同一时间轴上，便于观察放量上涨/下跌等现象。
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = ['Source Han Serif SC', 'SimHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False
tmp = df_hengrui.loc['2023-01-01':'2023-12-31'].copy()
fig, ax1 = plt.subplots(figsize=(12, 6))
ax1.plot(tmp.index, tmp['adj_close'], color='#1f77b4', linewidth=1.2, label='后复权收盘价')
ax1.set_xlabel('日期')
ax1.set_ylabel('价格(元)')
ax1.grid(True, alpha=0.25)
ax2 = ax1.twinx()
ax2.bar(tmp.index, tmp['volume'], color='#ff7f0e', alpha=0.25, label='成交量')
ax2.set_ylabel('成交量')
# 合并图例
lines1, labels1 = ax1.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax1.legend(lines1 + lines2, labels1 + labels2, loc='upper left')
plt.title('恒瑞医药(600276.SH)：价格与成交量')
plt.show()
到这里，你已经把“从数据快照读取 → 构造收益率 → 统计度量 → 可视化”的最小闭环跑通。后续章节会在这个闭环上叠加更严格的模型假设、估计方法与风险解释。