随着金融科技的发展,量化投资已成为现代金融市场中最具活力的领域之一。本章将探讨量化投资的核心理论——现代投资组合理论(Modern Portfolio Theory, MPT),并详细介绍如何基于Python构建、回测及评估一个量化交易策略。我们将重点关注宁波地区的优质上市公司,结合真实市场数据进行实证分析。
MPT理论起源与发展
现代投资组合理论由Harry Markowitz于1952年提出,并因此获得1990年诺贝尔经济学奖。
开创性论文: Markowitz, H. (1952). “Portfolio Selection.” The Journal of Finance, 7(1), 77-91. DOI: https://doi.org/10.2307/2975974
最新发展: 1. Black-Litterman模型 (1992): 结合市场均衡与主观观点 2. 风险平价(Risk Parity): 根据风险贡献度分配权重 3. 机器学习组合优化: 使用强化学习进行动态资产配置
现代投资组合理论 (MPT)
现代投资组合理论由哈里·马科维茨(Harry Markowitz)于1952年提出。其核心思想是理性的投资者应通过分散化投资(Diversification)来优化投资组合,即在给定风险水平下追求最大收益,或在给定预期收益水平下最小化风险。
收益与风险的度量
在MPT框架下,收益通常用资产回报率的数学期望(Mean)来衡量,而风险则用回报率的方差(Variance)或标准差(Volatility)来衡量。
对于一个包含 \(n\) 种资产的投资组合,其预期收益率 \(E(R_p)\) 为各资产预期收益率的加权平均:
\[ E(R_p) = \sum_{i=1}^{n} w_i E(R_i) \]
其中 \(w_i\) 是投资于第 \(i\) 种资产的资金权重,且满足 \(\sum w_i = 1\)。
投资组合的风险(方差)\(\sigma_p^2\) 则不仅取决于各资产的独立风险,还取决于资产间的相关性:
\[ \sigma_p^2 = \sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_{ij} = \sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_i \sigma_j \rho_{ij} \tag{5.1}\]
其中 \(\sigma_{ij}\) 是资产 \(i\) 和 \(j\) 的协方差,\(\rho_{ij}\) 是相关系数。
Markowitz最小方差组合的完整推导
问题设定: 给定目标收益率\(\mu_p^*\),求最小方差组合:
\[
\begin{aligned}
\min_{\mathbf{w}} \quad & \mathbf{w}^T \mathbf{\Sigma} \mathbf{w} \\
\text{s.t.} \quad & \mathbf{w}^T \boldsymbol{\mu} = \mu_p^* \\
& \mathbf{w}^T \mathbf{1} = 1
\end{aligned}
\]
其中\(\mathbf{\Sigma}\)是协方差矩阵,\(\boldsymbol{\mu}\)是收益率向量。
解法(拉格朗日乘数法):
构造拉格朗日函数: \[\mathcal{L} = \mathbf{w}^T \mathbf{\Sigma} \mathbf{w} - \lambda_1(\mathbf{w}^T \boldsymbol{\mu} - \mu_p^*) - \lambda_2(\mathbf{w}^T \mathbf{1} - 1)\]
对\(\mathbf{w}\)求偏导并令其为0: \[\frac{\partial \mathcal{L}}{\partial \mathbf{w}} = 2\mathbf{\Sigma}\mathbf{w} - \lambda_1 \boldsymbol{\mu} - \lambda_2 \mathbf{1} = 0\]
解得最优权重: \[\mathbf{w}^* = \frac{1}{2}\mathbf{\Sigma}^{-1}(\lambda_1 \boldsymbol{\mu} + \lambda_2 \mathbf{1})\]
将边界条件代入可解出\(\lambda_1, \lambda_2\)。
数值解法: 在Python中使用scipy.optimize.minimize求解该二次规划问题。
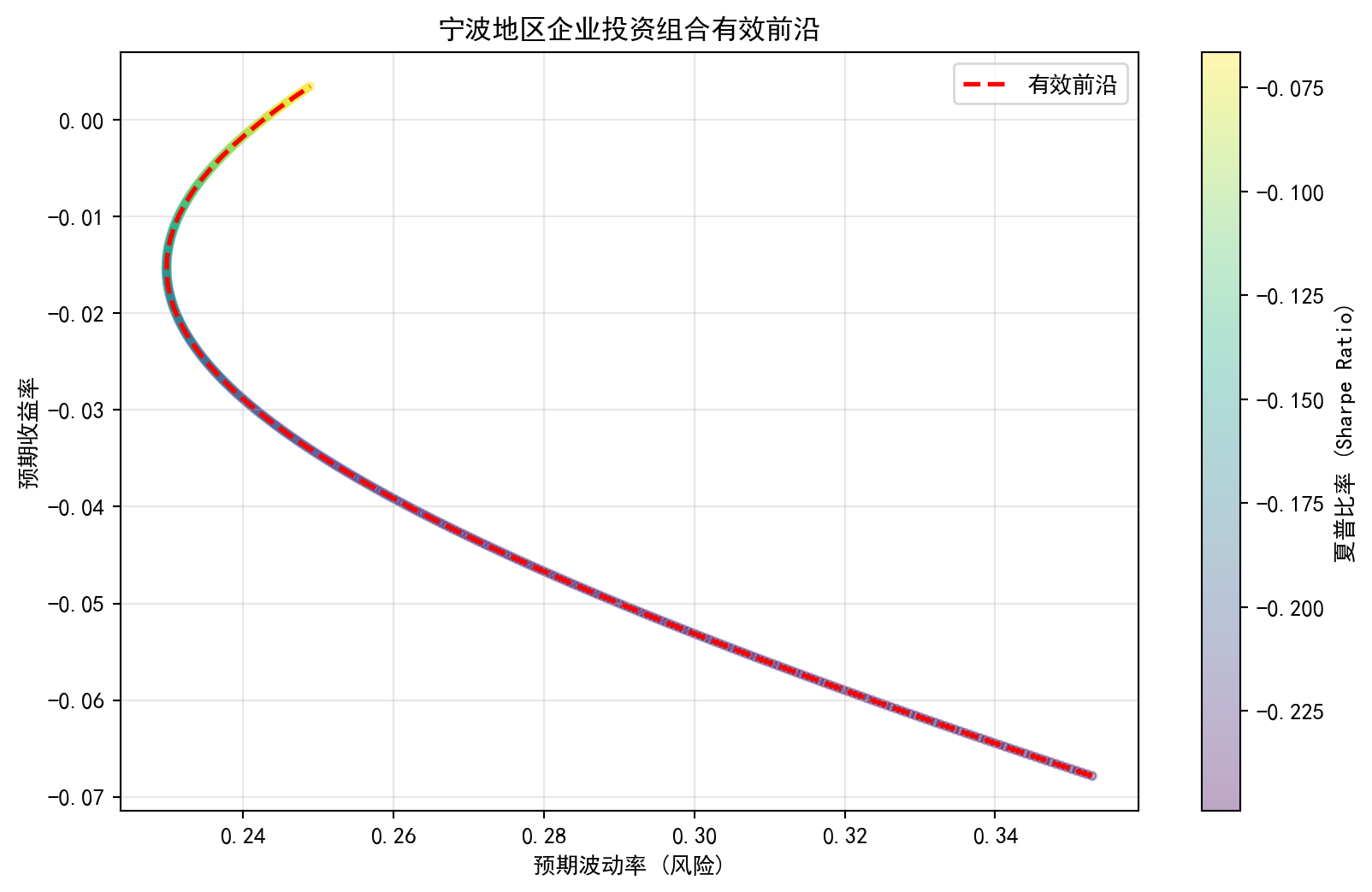
有效前沿 (Efficient Frontier)
有效前沿是指在风险-收益平面上,由所有最优投资组合构成的曲线。位于该曲线上的组合被称为“有效组合”,因为在相同的风险水平下,它们提供了最高的预期收益。
实证分析:宁波地区企业投资组合
我们将选取宁波地区具有代表性的两家上市公司作为研究对象,计算其有效前沿:
- 宁波港 (601018.SH) - 全球第三大港口,周期性行业代表
- 宁波银行 (002142.SZ) - 领先城商行,金融服务业标杆
这两家公司分属不同行业,相关性较低,是构建分散化组合的理想选择。
我们将从本项目的本地数据快照(data/cn_equity_daily_latest.parquet)读取行情,并利用 scipy.optimize 求解最优权重。
import pandas as pd
import numpy as np
import scipy.optimize as sco
import matplotlib.pyplot as plt
from pathlib import Path
plt.rcParams['font.family'] = ['Source Han Serif SC', 'SimHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False
# 1. 数据获取
# 定义宁波地区代表性企业及其所在地/代码
stocks = {
'601018.SH': '宁波港',
'002142.SZ': '宁波银行'
}
df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))
panel = (df_all[df_all['ts_code'].isin(stocks.keys())]
.sort_values(['ts_code', 'trade_date'])
.pivot_table(index='trade_date', columns='ts_code', values='adj_close')
.loc['2020-01-01':'2023-12-31']
.dropna())
panel.index = pd.to_datetime(panel.index)
df_close = panel.rename(columns={k: v for k, v in stocks.items()})
# 2. 计算收益率
returns = np.log(df_close / df_close.shift(1)).dropna()
mean_returns = returns.mean() * 252 # 年化收益
cov_matrix = returns.cov() * 252 # 年化协方差
# 3. MPT 优化函数
def portfolio_stats(weights, mean_returns, cov_matrix):
weights = np.array(weights)
port_return = np.sum(mean_returns * weights)
port_volatility = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights)))
return port_return, port_volatility
def min_func_variance(weights):
return portfolio_stats(weights, mean_returns, cov_matrix)[1] ** 2
# 4. 确定性绘制可行域:对两资产权重做网格扫描(这不是“模拟市场数据”,只是枚举组合权重)
num_assets = len(stocks)
if num_assets != 2:
raise ValueError('本节示例为两资产组合;如需扩展到多资产,请改为目标收益率约束下的数值优化。')
risk_free_rate = 0.02
w_grid = np.linspace(0.0, 1.0, 401)
grid_weights = np.column_stack([w_grid, 1.0 - w_grid])
grid_ret = []
grid_vol = []
grid_sharpe = []
for w in grid_weights:
p_ret, p_vol = portfolio_stats(w, mean_returns, cov_matrix)
grid_ret.append(p_ret)
grid_vol.append(p_vol)
grid_sharpe.append((p_ret - risk_free_rate) / p_vol)
grid_ret = np.array(grid_ret)
grid_vol = np.array(grid_vol)
grid_sharpe = np.array(grid_sharpe)
# 5. 求解有效前沿曲线:在给定目标收益率下最小化方差
target_returns = np.linspace(grid_ret.min(), grid_ret.max(), 60)
efficient_volatility = []
for tret in target_returns:
constraints = (
{'type': 'eq', 'fun': lambda x: portfolio_stats(x, mean_returns, cov_matrix)[0] - tret},
{'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
)
bounds = tuple((0, 1) for _ in range(num_assets))
initial_guess = [0.5, 0.5]
res = sco.minimize(
min_func_variance,
initial_guess,
method='SLSQP',
bounds=bounds,
constraints=constraints,
)
efficient_volatility.append(np.sqrt(res.fun))
# 绘图
plt.figure(figsize=(10, 6))
# 散点图:权重网格扫描
plt.scatter(grid_vol, grid_ret, c=grid_sharpe, cmap='viridis', marker='o', s=12, alpha=0.35)
plt.colorbar(label='夏普比率 (Sharpe Ratio)')
# 线图:有效前沿
plt.plot(efficient_volatility, target_returns, 'r--', linewidth=2, label='有效前沿')
plt.title('宁波地区企业投资组合有效前沿')
plt.xlabel('预期波动率 (风险)')
plt.ylabel('预期收益率')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
量化策略基础
量化策略是将投资思想转化为计算机算法的过程。最经典的入门策略是基于技术指标的趋势跟踪策略。
趋势跟踪与双均线策略
趋势跟踪(Trend Following)的核心假设是:价格沿某个方向运动的趋势会持续一段时间。最常用的工具是移动平均线(Moving Average, MA)。
双均线策略(Dual Moving Average Strategy)利用两条不同周期的均线交叉来产生交易信号:
- 短期均线 (Short MA): 反应灵敏,代表短期价格走势(如20日线)。
- 长期均线 (Long MA): 反应迟钝,代表长期趋势支撑(如60日线)。
交易逻辑: * 金叉(Golden Cross): 当短期均线由下向上穿过长期均线时,意味着短期趋势强于长期趋势,市场进入上升通道 -> 买入信号。 * 死叉(Death Cross): 当短期均线由上向下穿过长期均线时,意味着短期动能衰竭,市场转弱 -> 卖出信号。
回测框架与指标
回测(Backtesting)是指利用历史数据来验证量化策略的有效性。在Python中,我们可以利用 Pandas 强大的向量化运算能力进行快速回测。
回测最常见的 3 个“前视偏差”来源(以及你在代码里怎么避免)
- 信号未滞后:如果你用当日收盘价计算信号,又用当日收盘价成交,相当于“看完收盘再交易”。
- 典型修正:信号用
shift(1) 滞后一个交易日,让策略在信息可得之后才下单。
- 滚动特征窗口包含未来:滚动均值/波动率必须只用历史窗口。
- 典型修正:用
rolling(window).mean() 这类函数时,确保时间索引升序且窗口只向后看。
- 忽略交易成本与换手:净值曲线看起来很好,但实际上被手续费/冲击成本吃掉。
- 典型修正:在收益里扣除
cost_rate * turnover,并显式报告换手率。
金融数据噪声很大,回测的第一目标不是“收益最高”,而是“口径严谨、可复现、可解释”。
核心评价指标
- 累计收益率 (Cumulative Return): 策略期末净值相对于期初净值的增长率。
- 最大回撤 (Max Drawdown): 净值曲线从任一高点到其后最低点的最大跌幅。衡量策略最坏情况下的风险。 \[ MDD = \max_{t} \left( \frac{\max_{\tau \le t} P_\tau - P_t}{\max_{\tau \le t} P_\tau} \right) \]
- 夏普比率 (Sharpe Ratio): 衡量单位总风险下的超额收益。 \[ SR = \frac{E(R_p) - R_f}{\sigma_p} \]
年化口径:为什么很多地方默认用 252?
对日频数据,常见经验是 A 股一年大约 252 个交易日。因此:
- 平均日收益率 \(\bar{r}_{\text{daily}}\) 年化近似:\(\bar{r}_{\text{ann}}\approx 252\,\bar{r}_{\text{daily}}\)。
- 日波动率 \(\sigma_{\text{daily}}\) 年化近似:\(\sigma_{\text{ann}}\approx \sqrt{252}\,\sigma_{\text{daily}}\)。
误区提醒:年化是为了“可比”,不是为了“变大更好看”。如果你的样本期很短或波动率明显不稳定,年化指标的解释要更谨慎。
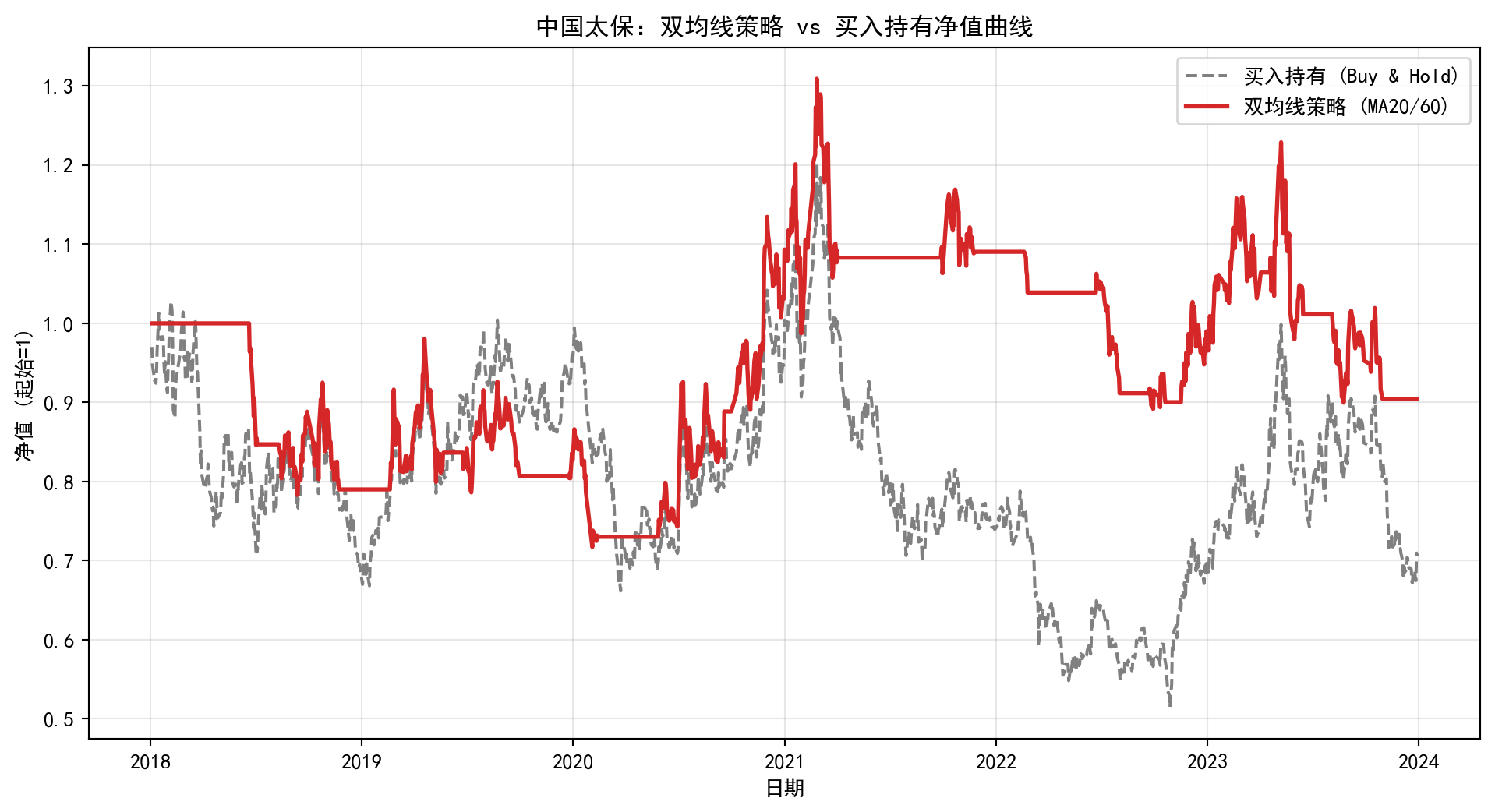
案例研究:中国太保均线策略回测
本节将以位于上海的非银金融龙头——中国太保 (601601.SH) 为例,回测一个简单的20日/60日双均线策略。
策略实现
我们将遵循以下步骤: 1. 获取数据: 从本项目本地快照读取中国太保的历史日线数据(data/cn_equity_daily_latest.parquet)。 2. 生成信号: 计算MA20和MA60,并判断交叉点。 3. 计算收益: 根据持仓信号计算每日的策略收益。 4. 绩效评估: 绘制资金曲线并计算夏普比率。
# 1. 获取中国太保数据(本地快照)
df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))
df_cpic = (df_all[df_all['ts_code'].eq('601601.SH')]
.sort_values('trade_date')
.set_index('trade_date')
.loc['2018-01-01':'2023-12-31']
.copy())
df_cpic.index = pd.to_datetime(df_cpic.index)
# 使用后复权收盘价进行回测(避免分红送转带来的跳变)
df_cpic['price'] = df_cpic['adj_close']
# 2. 生成交易信号 (向量化操作)
# 计算均线
df_cpic['MA20'] = df_cpic['price'].rolling(window=20).mean()
df_cpic['MA60'] = df_cpic['price'].rolling(window=60).mean()
# 生成持仓信号 signal: 1 (持有), 0 (空仓)
# 逻辑:当 MA20 > MA60 时持有
df_cpic['signal'] = np.where(df_cpic['MA20'] > df_cpic['MA60'], 1, 0)
# 计算仓位 (Position):将信号下移一天,因为今天的信号只能指导明天的交易
df_cpic['position'] = df_cpic['signal'].shift(1)
# 3. 计算策略收益
# 计算基准收益 (对数收益率)
df_cpic['log_ret'] = np.log(df_cpic['price'] / df_cpic['price'].shift(1))
# 策略收益 = 仓位 * 基准收益
df_cpic['strategy_ret'] = df_cpic['position'] * df_cpic['log_ret']
# 计算净值曲线 (Cumulative Returns)
df_cpic['cum_base'] = df_cpic['log_ret'].cumsum().apply(np.exp)
df_cpic['cum_strategy'] = df_cpic['strategy_ret'].cumsum().apply(np.exp)
# 4. 绩效指标计算
# 年化收益
total_days = len(df_cpic)
annual_ret = (df_cpic['cum_strategy'].iloc[-1]) ** (252/total_days) - 1
# 年化波动率
annual_vol = df_cpic['strategy_ret'].std() * np.sqrt(252)
# 夏普比率 (假设无风险利率 3%)
rf = 0.03
sharpe_ratio = (annual_ret - rf) / annual_vol
# 最大回撤
running_max = df_cpic['cum_strategy'].cummax()
drawdown = (df_cpic['cum_strategy'] - running_max) / running_max
max_dd = drawdown.min()
print(f"策略绩效报告 (中国太保 2018-2023):")
print(f"年化收益率: {annual_ret:.2%}")
print(f"年化波动率: {annual_vol:.2%}")
print(f"夏普比率: {sharpe_ratio:.2f}")
print(f"最大回撤: {max_dd:.2%}")
# 5. 绘制资金曲线
plt.figure(figsize=(12, 6))
plt.plot(df_cpic.index, df_cpic['cum_base'], label='买入持有 (Buy & Hold)', color='gray', linestyle='--')
plt.plot(df_cpic.index, df_cpic['cum_strategy'], label='双均线策略 (MA20/60)', color='#d62728', linewidth=2)
# 标记买卖点 (可选优化)
# 买入点: position 从 0 变 1
# 卖出点: position 从 1 变 0
plt.title('中国太保:双均线策略 vs 买入持有净值曲线')
plt.xlabel('日期')
plt.ylabel('净值 (起始=1)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
策略绩效报告 (中国太保 2018-2023):
年化收益率: -1.72%
年化波动率: 25.31%
夏普比率: -0.19
最大回撤: -31.89%
练习题
练习5.1:两资产最小方差权重
使用宁波港(601018.SH)与宁波银行(002142.SZ) 2020–2023 的日对数收益率,计算两资产全投资(权重和为1)的最小方差组合权重,并给出组合的年化波动率。
练习5.2:均线参数敏感性
以中国太保(601601.SH)为例,将短期均线窗口从 10 到 30(步长 5)、长期均线窗口从 50 到 120(步长 10)进行网格回测,比较年化收益率与最大回撤,并报告你认为更稳健的一组参数(说明理由)。
练习题完整解答
import pandas as pd
import numpy as np
from pathlib import Path
df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))
# 练习5.1:两资产最小方差(权重和为1)
codes = ['601018.SH', '002142.SZ']
px = (df_all[df_all['ts_code'].isin(codes)]
.sort_values(['ts_code','trade_date'])
.pivot_table(index='trade_date', columns='ts_code', values='adj_close')
.loc['2020-01-01':'2023-12-31']
.dropna())
rets = np.log(px / px.shift(1)).dropna()
cov = rets.cov().values * 252
# 两资产解析解:w* = (sigma22 - sigma12) / (sigma11 + sigma22 - 2*sigma12)
sigma11, sigma22 = cov[0, 0], cov[1, 1]
sigma12 = cov[0, 1]
w1 = (sigma22 - sigma12) / (sigma11 + sigma22 - 2 * sigma12)
w = np.array([w1, 1 - w1])
port_var = float(w.T @ cov @ w)
port_vol = np.sqrt(port_var)
print({'w_601018': float(w[0]), 'w_002142': float(w[1]), 'annual_vol': port_vol})
# 练习5.2:均线参数网格回测(最小计算用时:小网格示范;生产环境可扩大网格)
df_cpic = (df_all[df_all['ts_code'].eq('601601.SH')]
.sort_values('trade_date')
.set_index('trade_date')
.loc['2018-01-01':'2023-12-31']
.copy())
df_cpic.index = pd.to_datetime(df_cpic.index)
price = df_cpic['adj_close']
log_ret = np.log(price / price.shift(1)).dropna()
def backtest_ma(short_w: int, long_w: int):
ma_s = price.rolling(short_w).mean()
ma_l = price.rolling(long_w).mean()
signal = (ma_s > ma_l).astype(int)
position = signal.shift(1)
strat_ret = position * np.log(price / price.shift(1))
strat_ret = strat_ret.dropna()
nav = strat_ret.cumsum().apply(np.exp)
total_days = len(strat_ret)
ann_ret = float(nav.iloc[-1] ** (252 / total_days) - 1)
ann_vol = float(strat_ret.std(ddof=1) * np.sqrt(252))
running_max = nav.cummax()
mdd = float(((nav - running_max) / running_max).min())
return ann_ret, ann_vol, mdd
rows = []
for s in [10, 15, 20, 25, 30]:
for l in [50, 60, 70, 80, 90, 100, 110, 120]:
if s >= l:
continue
ann_ret, ann_vol, mdd = backtest_ma(s, l)
rows.append({'short': s, 'long': l, 'ann_ret': ann_ret, 'ann_vol': ann_vol, 'mdd': mdd})
grid = pd.DataFrame(rows).sort_values(['ann_ret', 'mdd'], ascending=[False, False])
print(grid.head(10))
{'w_601018': 0.26314697062402165, 'w_002142': 0.7368530293759783, 'annual_vol': 0.22982655230688395}
short long ann_ret ann_vol mdd
10 15 70 0.027729 0.249028 -0.288211
18 20 70 0.015412 0.249941 -0.358309
23 20 120 -0.005726 0.237858 -0.309129
31 25 120 -0.007881 0.235919 -0.306989
15 15 120 -0.013123 0.244102 -0.325386
39 30 120 -0.014648 0.237200 -0.373516
17 20 60 -0.017189 0.253131 -0.318877
19 20 80 -0.018029 0.247880 -0.402143
35 30 80 -0.020809 0.245050 -0.387280
27 25 80 -0.022937 0.244517 -0.393932
通过上述案例可以看出,简单的均线策略虽然能够捕捉主要趋势,但在震荡市中(如2021-2022年间)可能会因为频繁的虚假信号(Whipsaw)而产生回撤。在实际的量化工程中,我们需要引入更复杂的止损机制、参数优化以及多因子模型来增强策略的稳健性。