4  金融风险评估与管理

金融风险管理是现代金融工程的核心领域之一。在日益复杂的金融市场中，有效地识别、量化和控制风险对于金融机构和投资者至关重要。本章将重点介绍波动率建模、风险价值 (VaR) 以及预期亏损 (ES) 等核心概念，并结合宁波地区上市公司的实际数据进行实证分析。

注记

波动率建模理论起源

GARCH模型的理论基础源于:

  1. Engle, R. F. (1982). “Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation.” Econometrica, 50(4), 987-1007.
    • 提出ARCH模型,因此获得2003年诺贝尔经济学奖
    • DOI: https://doi.org/10.2307/1912773
  2. Bollerslev, T. (1986). “Generalized Autoregressive Conditional Heteroskedasticity.” Journal of Econometrics, 31(3), 307-327.
    • 将ARCH扩展为GARCH,极大提高了模型的灵活性
    • DOI: https://doi.org/10.1016/0304-4076(86)90063-1

最新发展: - EGARCH/GJR-GARCH: 处理杠杆效应(非对称性) - Realized GARCH: 结合高频已实现波动率 - DCC-GARCH: 动态条件相关模型

4.1 波动率建模

在金融时间序列中，资产收益率的波动率往往不是恒定的，而是随时间变化的。理解波动率的动态特征对于风险管理、期权定价和投资组合配置至关重要。

4.1.1 收益率的典型事实 (Stylized Facts)

大量的实证研究表明，金融资产收益率序列通常表现出以下典型事实：

  1. 尖峰厚尾 (Fat Tails): 收益率的分布往往比正态分布具有更高的峰度和更厚的尾部，意味着极端事件发生的概率比正态分布预期的要高。
  2. 波动率聚集 (Volatility Clustering): 大幅度的波动后面往往紧接着大幅度的波动，小幅度的波动后面往往紧接着小幅度的波动。这意味着波动率具有正自相关性。
  3. 杠杆效应 (Leverage Effect): 价格下跌往往比同等幅度的价格上涨带来更大的波动率增加。
注记

“波动率聚集”到底是什么意思？和 GARCH 有什么一一对应关系？

波动率聚集可以用一句话概括：波动有“记忆”——昨天很剧烈，今天也更可能剧烈。

在 GARCH(1,1) 里，这种“记忆”由两条路径叠加形成：

  • \(\alpha r_{t-1}^2\)：把“昨天的冲击强度”带到今天（新闻冲击效应）。
  • \(\beta \sigma_{t-1}^2\)：把“昨天的波动水平”延续到今天（持续性）。

一个实务经验是：如果 \(\alpha+\beta\) 非常接近 1，表示波动率冲击衰减很慢；这与我们在金融市场里常见的“风暴过后余波仍在”相吻合。

4.1.2 ARCH 与 GARCH 模型

为了捕捉上述特征，Engle (1982) 提出了自回归条件异方差 (ARCH) 模型，Bollerslev (1986) 将其推广为广义自回归条件异方差 (GARCH) 模型。

最常用的 GARCH(1,1) 模型定义如下：

设 \(r_t\) 为 \(t\) 时刻的资产对数收益率，假设其均值为 0，则：

\[ r_t = \sigma_t \epsilon_t \tag{4.1}\]

其中 \(\epsilon_t \sim i.i.d. N(0,1)\) 是标准化残差，\(\sigma_t^2\) 是条件方差，遵循以下演化过程：

\[ \sigma_t^2 = \omega + \alpha r_{t-1}^2 + \beta \sigma_{t-1}^2 \tag{4.2}\]

其中：

  • \(\omega > 0\): 常数项。
  • \(\alpha \ge 0\): ARCH 项系数，反映了近期冲击（新信息）对波动率的影响。
  • \(\beta \ge 0\): GARCH 项系数，反映了过去波动率对当前波动率的持续性影响。
  • 约束条件 \(\alpha + \beta < 1\) 保证了波动率过程的平稳性。
提示

GARCH(1,1)的完整推导与性质

1. 无条件方差的计算

对@eq-garch11两边取期望: \[E[\sigma_t^2] = \omega + \alpha E[r_{t-1}^2] + \beta E[\sigma_{t-1}^2]\]

由于\(E[r_t^2] = E[\sigma_t^2 \epsilon_t^2] = E[\sigma_t^2]\) (因为\(E[\epsilon_t^2]=1\)),且平稳性要求\(E[\sigma_t^2] = \sigma^2\)为常数,故:

\[\sigma^2 = \omega + (\alpha + \beta)\sigma^2\]

解得: \[\sigma^2 = \frac{\omega}{1 - \alpha - \beta}\]

这解释了为什么需要\(\alpha + \beta < 1\)。

2. 波动率聚集性

GARCH模型能够捕捉”大波动后跟着大波动”的特征。直观理解:如果\(r_{t-1}^2\)很大(昨天出现大幅波动),郣么\(\sigma_t^2\)也会增大(今天预期波动也大)。

3. 最大似然估计(MLE)

参数\(\theta = (\omega, \alpha, \beta)\)通过最大化对数似然函数估计: \[L(\theta) = \sum_{t=1}^{T} \log f(r_t | \mathcal{F}_{t-1}; \theta)\]

其中\(f\)是条件密度函数。对于正态假设: \[\log f(r_t | \mathcal{F}_{t-1}) = -\frac{1}{2}\log(2\pi) - \frac{1}{2}\log(\sigma_t^2) - \frac{r_t^2}{2\sigma_t^2}\]

4.1.3 实证分析：宁波港的波动率建模

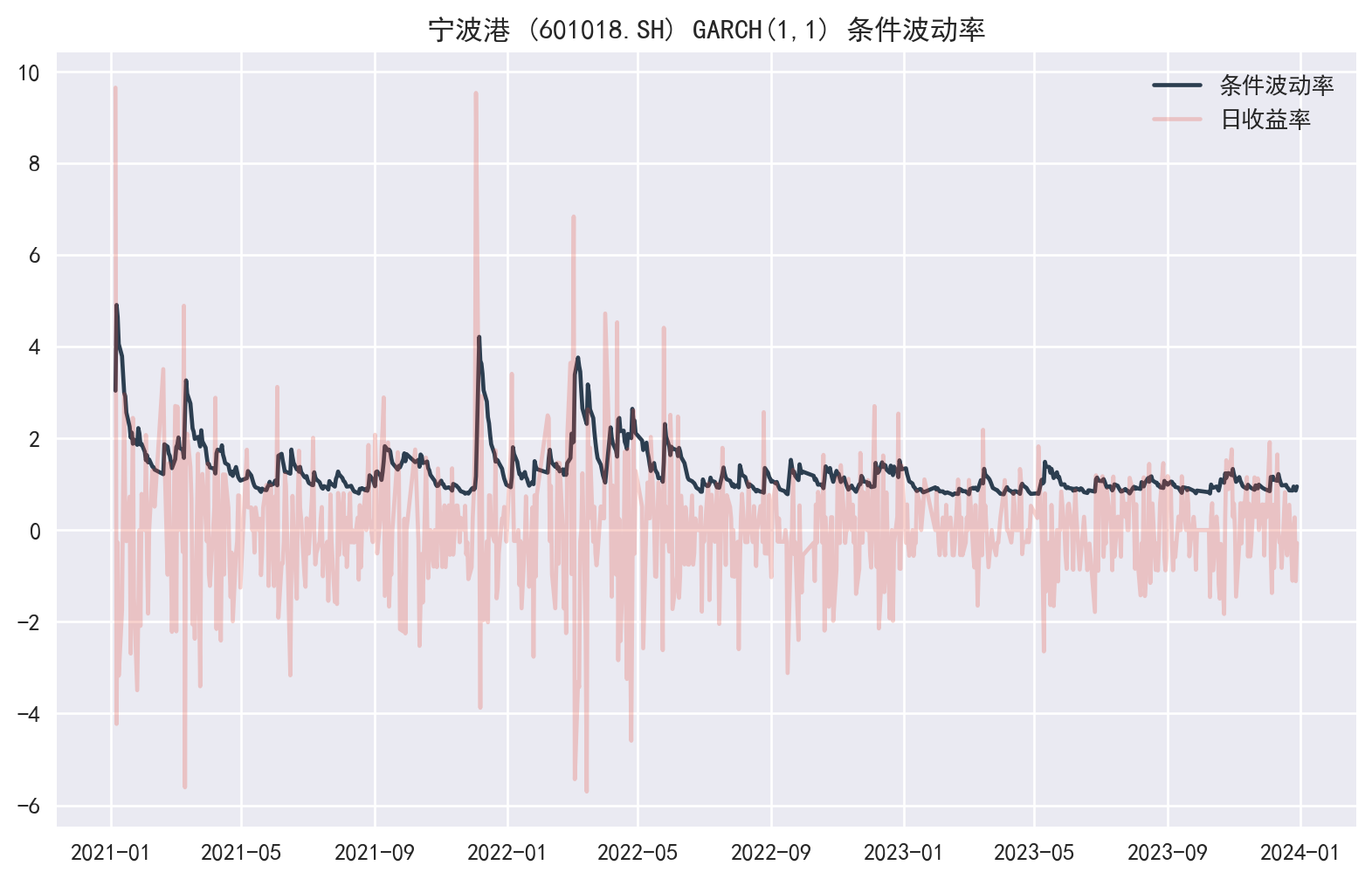
我们将使用Python的arch库，对宁波港(601018.SH)的日收益率进行GARCH(1,1)建模。宁波港作为全球第三大港口，其股价波动与国际贸易周期密切相关，是研究周期性行业风险的经典样本。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path
from arch import arch_model

plt.style.use('seaborn-v0_8')
plt.rcParams['font.family'] = ['Source Han Serif SC', 'SimHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False

df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))

# 1. 获取数据：宁波港 (601018.SH)
df = (df_all[df_all['ts_code'].eq('601018.SH')]
      .sort_values('trade_date')
      .set_index('trade_date')
      .loc['2021-01-01':'2023-12-31']
      .copy())

# 2. 计算对数收益率（乘以100便于数值优化；常见做法）
df['log_ret'] = np.log(df['adj_close'] / df['adj_close'].shift(1)) * 100
df = df.dropna(subset=['log_ret'])

# 3. 拟合 GARCH(1,1) 模型
am = arch_model(df['log_ret'], vol='Garch', p=1, q=1, dist='Normal')
res = am.fit(disp='off')

print(res.summary())

# 4. 绘制条件波动率
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(res.conditional_volatility, color='#2c3e50', label='条件波动率')
ax.plot(df['log_ret'], color='#e74c3c', alpha=0.25, label='日收益率')
ax.set_title('宁波港 (601018.SH) GARCH(1,1) 条件波动率')
ax.legend()
plt.show()
                     Constant Mean - GARCH Model Results                      
==============================================================================
Dep. Variable:                log_ret   R-squared:                       0.000
Mean Model:             Constant Mean   Adj. R-squared:                  0.000
Vol Model:                      GARCH   Log-Likelihood:               -1160.45
Distribution:                  Normal   AIC:                           2328.90
Method:            Maximum Likelihood   BIC:                           2347.25
                                        No. Observations:                  726
Date:                Sun, Jan 18 2026   Df Residuals:                      725
Time:                        22:26:30   Df Model:                            1
                                  Mean Model                                  
==============================================================================
                  coef    std err          t      P>|t|       95.0% Conf. Int.
------------------------------------------------------------------------------
mu         -8.7693e-03  4.328e-02     -0.203      0.839 [-9.360e-02,7.606e-02]
                            Volatility Model                            
========================================================================
                 coef    std err          t      P>|t|  95.0% Conf. Int.
------------------------------------------------------------------------
omega          0.1204      0.133      0.902      0.367 [ -0.141,  0.382]
alpha[1]       0.1822      0.151      1.208      0.227 [ -0.113,  0.478]
beta[1]        0.7562      0.191      3.965  7.355e-05 [  0.382,  1.130]
========================================================================

Covariance estimator: robust

提示

为什么很多 GARCH 例子会把收益率乘以 100？

这是一个纯粹的数值优化技巧：把日对数收益率从“0.01 量级”拉到“1 量级”，能让极大似然估计的优化器更稳定、更快收敛。乘以 100 不会改变序列的相对形态，只会改变参数的数值尺度。

与代码对应：这里 * 100 的目的就是提升 arch_model(...).fit() 的数值稳定性。

从模型结果中，我们可以观察到 \(\alpha\) 和 \(\beta\) 的估计值。通常 \(\beta\) 值较大（接近 0.9），表明波动率具有很强的持续性（clustering）。

4.2 风险价值 (VaR) 与 预期亏损 (ES)

4.2.1 概念定义

风险价值 (Value at Risk, VaR) 是衡量金融资产组合在特定置信水平 \(\alpha\) (例如 95% 或 99%) 和特定持有期内可能遭受的最大损失。数学上，VaR 定义为损失分布的 \(\alpha\) 分位数。

设 \(L\) 为投资组合在持有期内的损失（正值表示亏损），则置信水平为 \(1-\alpha\) 的 VaR 满足：

\[ P(L \le \text{VaR}_{1-\alpha}) = 1 - \alpha \]

或者，如果着眼于收益率分布 \(R\)，且 \(\text{VaR}\) 表示为负收益阈值，则：

\[ P(R < -\text{VaR}_{1-\alpha}) = \alpha \]

预期亏损 (Expected Shortfall, ES)，也称为条件风险价值 (CVaR)，定义为超过 VaR 水平的损失的期望值。ES 克服了 VaR 不满足次可加性（Sub-additivity）的缺点，是一个一致性风险度量指标。

\[ \text{ES}_{1-\alpha} = E[L \mid L > \text{VaR}_{1-\alpha}] \]

注记

不要被符号“绕晕”：VaR/ES 是在度量‘损失’还是‘收益’？

  • 在风险管理里，最稳妥的做法是先把变量统一成“损失”\(L\)（亏损为正数），然后 VaR/ES 都是 损失分布 的尾部统计量。
  • 如果你用的是“收益率”\(R\)（盈利为正），那么 VaR 往往写成一个 负收益阈值 的绝对值（例如“最坏 5% 情况下，收益率会低于 \(-\text{VaR}\)”）。

本章后续代码里，我们会显式构造 loss_distribution = -portfolio_hist_returns，就是把收益率转成损失，避免口径混用。

4.2.2 风险度量图示

下图展示了正态分布下的 VaR 与尾部风险。阴影部分代表了发生概率仅为 5% 的极端亏损区域。

收益率 0（均值） -VaR（95%） 尾部风险（5%） ES / CVaR
图 4.1: 风险价值 (VaR) 与尾部风险示意图

4.2.3 计算方法

  1. 参数法 (Parametric Method): 假设收益率服从特定的分布（如正态分布）。计算公式为 \(\text{VaR} = |\mu - z_{\alpha} \sigma| \times \text{Value}\)。
  2. 历史模拟法 (Historical Simulation): 直接根据历史收益率数据的经验分布来确定分位数，不假设特定分布。
  3. 蒙特卡洛模拟法 (Monte Carlo Simulation): 通过模拟价格路径生成成千上万种可能的情景，统计损益分布。
注意

持有期从 1 天变成 10 天：什么时候能用“平方根法则”？

你可能见过一个常用近似：如果单日损失（或收益）独立同分布且方差稳定，那么 \[\sigma_{T}\approx \sqrt{T}\,\sigma_{1}\] 进而可以把 1 日 VaR 近似放大到 \(T\) 日。

但在金融风险管理里，这个近似有清晰的适用边界：

  • 更可靠的前提：短期收益近似独立、波动率不随时间剧烈变化。
  • 容易失效的场景：波动率聚集（本章正要用 GARCH 处理）、极端尾部（厚尾分布）、流动性冲击。

与代码对应：本章主要计算单日 VaR/ES；如果你需要多日持有期，建议用“滚动历史法/蒙特卡洛/GARCH 预测方差再聚合”等更稳健的方法，而不是机械套用 \(\sqrt{T}\)。

4.3 案例研究：长三角投资组合风险管理

为了体现长三角地区在金融、科技和医药领域的协同发展，我们构建一个包含三只长三角地区代表性股票的投资组合，并计算其风险指标。

投资组合构成: 1. 银行: 上海银行 (601229.SH) - 总部位于上海，长三角核心金融机构。 2. 科技: 中芯国际 (688981.SH) - 总部位于上海，中国内地晶圆代工龙头。 3. 医药: 恒瑞医药 (600276.SH) - 总部位于江苏连云港，创新药龙头。

4.3.1 数据获取与预处理

import pandas as pd
import numpy as np
from pathlib import Path

df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))

# 定义股票代码（长三角代表）
tickers = {
    '上海银行': '601229.SH',
    '中芯国际': '688981.SH',
    '恒瑞医药': '600276.SH',
}

prices = (df_all[df_all['ts_code'].isin(tickers.values())]
          .sort_values(['ts_code','trade_date'])
          .pivot_table(index='trade_date', columns='ts_code', values='adj_close')
          .loc['2021-01-01':'2023-12-31']
          .dropna())

portfolio_prices = prices.rename(columns={v: k for k, v in tickers.items()})
portfolio_returns = np.log(portfolio_prices / portfolio_prices.shift(1)).dropna()

# 假设等权重配置
weights = np.array([1/3, 1/3, 1/3])
initial_investment = 1_000_000  # 假设投资 100 万元

4.3.2 组合风险计算

我们将分别使用参数法（正态分布假设）和历史模拟法计算该投资组合在 95% 置信水平下的单日 VaR。

# 1. 计算组合的历史日收益率序列
# R_p = w1*R1 + w2*R2 + w3*R3
portfolio_hist_returns = portfolio_returns.dot(weights)

# 2. 参数法 VaR (Normal VaR)
mu_p = portfolio_hist_returns.mean()
sigma_p = portfolio_hist_returns.std()
confidence_level = 0.95

# 正态分布分位数 (单尾)
from scipy.stats import norm
z_score = norm.ppf(1 - confidence_level) # 约为 -1.645

var_parametric_pct = -(mu_p + z_score * sigma_p)
var_parametric_value = var_parametric_pct * initial_investment

# 3. 历史模拟法 VaR (Historical VaR)
var_historical_pct = -np.percentile(portfolio_hist_returns, (1 - confidence_level) * 100)
var_historical_value = var_historical_pct * initial_investment

# 4. 预期亏损 (ES) - 历史法
loss_distribution = -portfolio_hist_returns
es_historical_pct = loss_distribution[loss_distribution > var_historical_pct].mean()
es_historical_value = es_historical_pct * initial_investment

# 展示结果
result_df = pd.DataFrame({
    '指标': ['参数法 VaR (95%)', '历史法 VaR (95%)', '历史法 ES (95%)'],
    '百分比风险': [f"{var_parametric_pct:.4%}", f"{var_historical_pct:.4%}", f"{es_historical_pct:.4%}"],
    '金额风险 (万元)': [f"{var_parametric_value/10000:.2f}", f"{var_historical_value/10000:.2f}", f"{es_historical_value/10000:.2f}"]
})

print("长三角投资组合风险评估报告 (持有期: 1天, 置信度: 95%)")
print("-" * 50)
print(result_df.to_markdown(index=False))
print("-" * 50)
print(f"组合波动率 (年化): {sigma_p * np.sqrt(252):.2%}")
长三角投资组合风险评估报告 (持有期: 1天, 置信度: 95%)
--------------------------------------------------
| 指标             | 百分比风险   |   金额风险 (万元) |
|:-----------------|:-------------|------------------:|
| 参数法 VaR (95%) | 1.9818%      |              1.98 |
| 历史法 VaR (95%) | 1.7997%      |              1.8  |
| 历史法 ES (95%)  | 2.6939%      |              2.69 |
--------------------------------------------------
组合波动率 (年化): 18.73%

4.3.3 结果解读

  • 参数法 vs 历史法: 如果历史法计算出的 VaR 显著高于参数法，说明收益率分布存在“厚尾”特征，正态分布假设低估了风险。
  • ES 的重要性: 还可以看到，ES（预期亏损）的数值总是大于 VaR。这意味着一旦击穿了 VaR 阈值，平均损失将达到 ES 所显示的水平。对于风险厌恶的管理者来说，关注 ES 比单纯关注 VaR 更能防范极端黑天鹅事件。

长三角地区企业在经济周期中表现出较强的韧性，但特定行业（如科技和医药）的高波动性依然要求我们在构建组合时引入严格的风险预算和动态对冲策略。

4.4 练习题

练习4.1：GARCH(1,1) 参数含义

对宁波港(601018.SH)拟合 GARCH(1,1)，报告 ω、α、β，并说明 α+β 与波动率持续性的关系。

练习4.2：VaR 与 ES 的对比

对一个等权组合（宁波港 601018.SH、宁波银行 002142.SZ、恒瑞医药 600276.SH）计算 95% 单日 VaR（参数法与历史法）以及历史法 ES，并解释为什么 ES 通常大于 VaR。

4.5 练习题完整解答

import pandas as pd
import numpy as np
from pathlib import Path
from arch import arch_model
from scipy.stats import norm

df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))

# 练习4.1：宁波港 GARCH(1,1)
df_port = (df_all[df_all['ts_code'].eq('601018.SH')]
           .sort_values('trade_date')
           .set_index('trade_date')
           .loc['2021-01-01':'2023-12-31']
           .copy())
r = np.log(df_port['adj_close'] / df_port['adj_close'].shift(1)).dropna() * 100
res = arch_model(r, vol='Garch', p=1, q=1, dist='Normal').fit(disp='off')
params = res.params
omega, alpha, beta = float(params['omega']), float(params['alpha[1]']), float(params['beta[1]'])
print(f'GARCH(1,1) 参数：omega={omega:.6f}, alpha={alpha:.4f}, beta={beta:.4f}, alpha+beta={alpha+beta:.4f}')

# 练习4.2：组合 VaR/ES
codes = ['601018.SH','002142.SZ','600276.SH']
px = (df_all[df_all['ts_code'].isin(codes)]
      .sort_values(['ts_code','trade_date'])
      .pivot_table(index='trade_date', columns='ts_code', values='adj_close')
      .loc['2021-01-01':'2023-12-31']
      .dropna())
rets = np.log(px / px.shift(1)).dropna()
w = np.array([1/3, 1/3, 1/3])
rp = rets.values @ w
mu, sigma = float(rp.mean()), float(rp.std(ddof=1))
cl = 0.95
z = norm.ppf(1 - cl)
var_param = -(mu + z * sigma)
var_hist = -np.percentile(rp, (1 - cl) * 100)
loss = -rp
es_hist = float(loss[loss > var_hist].mean())
print({'VaR_param(95%)': var_param, 'VaR_hist(95%)': var_hist, 'ES_hist(95%)': es_hist})
GARCH(1,1) 参数：omega=0.120421, alpha=0.1822, beta=0.7562, alpha+beta=0.9384
{'VaR_param(95%)': 0.022595889533541604, 'VaR_hist(95%)': 0.020983575250979346, 'ES_hist(95%)': 0.02980875965028416}