3  金融时间序列分析

金融时间序列分析是量化金融的基石。不同于横截面数据（Cross-sectional Data），时间序列数据具有内在的时间依赖性。理解这种依赖结构，对于资产定价、风险管理以及交易策略的构建至关重要。本章将从经典的线性模型出发，探讨平稳性、ARIMA 模型族及其在金融市场预测中的应用。

注记

时间序列分析理论起源

ARIMA模型的理论基础源于 Box 和 Jenkins 的开创性工作（可参见后续新版教材 Box 等 (2015)）。他们将时间序列分析从纯粹的描述性统计提升到了一个系统性的建模框架。

最新发展包括: - GARCH族模型 (Engle 1982, Bollerslev 1986): 处理波动率聚集性 - 向量ARIMA (VARIMA): 多变量时间序列建模 - 深度学习斶序模型: LSTM, Temporal CNN

经典文献: 1. Box, G. E. P., & Jenkins, G. M. (1976). Time Series Analysis: Forecasting and Control. Holden-Day. 2. Tsay, R. S. (2010). Analysis of Financial Time Series (3rd ed.). Wiley. DOI: 10.1002/9780470644560 3. Hamilton, J. D. (1994). Time Series Analysis. Princeton University Press.

3.1 时间序列理论基础

3.1.1 序列分解

一个典型的金融时间序列 \(X_t\) 通常可以分解为以下三个部分：

\[ X_t = T_t + S_t + \epsilon_t \]

其中： - \(T_t\) 表示趋势项（Trend），反映数据的长期运动方向（如经济增长带来的股市长期上涨）。 - \(S_t\) 表示季节项（Seasonality），反映周期性的波动（如财报季效应）。 - \(\epsilon_t\) 表示残差项（Noise/Irregular），包含随机波动。

3.1.2 平稳性 (Stationarity)

在经典时间序列分析中，弱平稳性（Weak Stationarity）是一个核心假设。一个时间序列 \(\{X_t\}\) 被称为弱平稳的，如果在满足以下条件：

  1. 均值恒定：对于所有 \(t\)，期望值 \(E[X_t] = \mu\) 为常数。
  2. 方差有限且恒定：对于所有 \(t\)，方差 \(Var(X_t) = \sigma^2\) 为有限常数。
  3. 自协方差仅依赖于滞后阶数：对于所有 \(t\) 和 \(k\)，协方差 \(Cov(X_t, X_{t+k}) = \gamma_k\) 仅与时间间隔 \(k\) 有关，而与具体时间 \(t\) 无关。

大多数金融资产价格（如股价 \(P_t\)）是非平稳的，通常表现为随机游走。然而，其对数收益率 \(r_t = \ln(P_t) - \ln(P_{t-1})\) 往往表现出平稳特征，这使得我们能够对其进行建模。

注记

弱平稳为什么重要？用一句话连接到本章代码

很多经典模型（AR/MA/ARIMA）隐含一个关键前提：序列的“统计特征”在样本期内相对稳定。

  • 直觉：如果均值/方差一直在漂移，模型学到的参数很可能只是在追随趋势，而不是学习可迁移的动态规律。
  • 常见做法：对价格 \(P_t\) 不直接建模，而是对收益率（尤其对数收益率）建模，因为收益率更接近“围绕 0 上下波动”的平稳过程。
  • 与代码对应：本章在 3.4.1 先构造 log_ret，并在 3.4.2 分别对 adj_close 与 log_ret 做 ADF 检验，帮助你直观看到“价格多半非平稳、收益率更可能平稳”。

3.1.3 单位根检验 (Unit Root Test)

为了检验序列的平稳性，最常用的统计方法是 Augmented Dickey-Fuller (ADF) 检验。

ADF 检验的原假设（\(H_0\)）是序列存在单位根（即非平稳）。 - 如果检验统计量的 \(p\) 值小于显著性水平（如 0.05），则拒绝原假设，认为序列是平稳的。 - 反之，则认为序列是非平稳的。

提示

ADF检验的数学推导

考虑AR(1)过程: \(X_t = \rho X_{t-1} + \epsilon_t\)

当\(|\rho| = 1\)时,过程非平稳(单位根)。将上式改写为: \[\Delta X_t = X_t - X_{t-1} = (\rho - 1)X_{t-1} + \epsilon_t = \delta X_{t-1} + \epsilon_t\]

其中\(\delta = \rho - 1\)。单位根检验等价于检验: - \(H_0: \delta = 0\) (非平稳) - \(H_1: \delta < 0\) (平稳)

ADF检验统计量: \[ADF = \frac{\hat{\delta}}{SE(\hat{\delta})}\]

其中Dickey-Fuller (1979)证明,在原假设下该统计量不遵从标准t分布,而是遵从一个非标准的分布,需要查专门的Dickey-Fuller临界值表。

Augmented指的是加入滞后项以处理高阶自相关: \[\Delta X_t = \delta X_{t-1} + \sum_{i=1}^{p}\gamma_i \Delta X_{t-i} + \epsilon_t\]

3.2 线性时间序列模型

3.2.1 自回归模型 AR(p)

自回归模型（AutoRegressive Model）假设当前值 \(X_t\) 线性依赖于其过去 \(p\) 个值。\(AR(p)\) 模型的数学定义为：

\[ X_t = c + \sum_{i=1}^{p} \phi_i X_{t-i} + \epsilon_t \]

其中 \(\phi_i\) 是自回归系数，\(\epsilon_t \sim WN(0, \sigma^2)\) 是白噪声序列。

3.2.2 移动平均模型 MA(q)

移动平均模型（Moving Average Model）假设当前值 \(X_t\) 线性依赖于过去 \(q\) 个白噪声冲击。\(MA(q)\) 模型的数学定义为：

\[ X_t = \mu + \epsilon_t + \sum_{j=1}^{q} \theta_j \epsilon_{t-j} \]

3.2.3 ARIMA(p,d,q) 模型

将 AR 和 MA 结合，我们得到 ARMA(p,q) 模型。若原始序列非平稳，需先进行 \(d\) 阶差分使其平稳，这便构成了 ARIMA(p,d,q) 模型（AutoRegressive Integrated Moving Average）。

其一般形式可表示为：

\[ \left(1 - \sum_{i=1}^{p} \phi_i L^i\right) (1 - L)^d X_t = c + \left(1 + \sum_{j=1}^{q} \theta_j L^j\right) \epsilon_t \]

其中 \(L\) 为滞后算子（Lag Operator），即 \(L^k X_t = X_{t-k}\)。

注意

差分 \(d\) 的两个误区：差得越多≠越好

差分的目标不是“让图看起来更随机”，而是把系统性的趋势/单位根成分剔除，让序列更接近平稳。

  • 直觉：\(\Delta X_t = X_t - X_{t-1}\) 把“水平”变成“变化”。对价格差分，本质上是在做简单收益率的近似。
  • 误区 1：过度差分。如果你对本来已经平稳的收益率再差分，可能引入不必要的噪声，让模型难以捕捉结构。
  • 误区 2：价格直接 ARIMA。对价格做 ARIMA 往往会把趋势当成可预测信号；实务里更常见的做法是对收益率建模，或对价格做协整/误差修正等更严谨的结构。

与代码对应：在本章案例中，我们直接对 log_ret 设定 order=(p,0,q)（即 \(d=0\)），因为收益率通常无需再差分。

3.3 Box-Jenkins 建模方法论

构建 ARIMA 模型通常遵循 Box-Jenkins 方法论，包含模型识别、参数估计、模型诊断和预测四个步骤。

1. 模型识别 (平稳性检验、ACF/PACF) 2. 参数估计 (MLE、AIC/BIC) 3. 模型诊断 (残差是否近似白噪声) 通过 未通过（回到识别） 4. 预测 (样本外检验、滚动预测)
图 3.1: Box-Jenkins 方法论流程图
注记

ACF / PACF 到底在看什么？（给第一次做时序的你）

  • ACF（自相关）：衡量 \(X_t\) 与 \(X_{t-k}\) 的线性相关性。它回答“过去 \(k\) 天和今天是不是一起涨跌”。
  • PACF（偏自相关）：在剔除 1 到 \(k-1\) 阶影响后，单独看 \(k\) 阶滞后对今天的“净贡献”。它回答“在考虑了更近几天以后，第 \(k\) 天之前还有没有额外信息”。

经验口诀（只是入门启发，不是定律）：

  • AR(p) 常见现象：PACF 在 \(p\) 阶后“截尾”，ACF “拖尾”。
  • MA(q) 常见现象：ACF 在 \(q\) 阶后“截尾”，PACF “拖尾”。

金融收益率往往信噪比很低，图形判别不一定稳定，所以实务里通常结合信息准则与样本外评估一起做。

提示

AIC/BIC 不是“越小越好”的玄学：它们在惩罚什么？

信息准则通常写成： \[\text{AIC} = -2\log\hat{L} + 2k,\qquad \text{BIC} = -2\log\hat{L} + k\log(n)\]

  • \(\hat{L}\) 是最大似然（拟合越好，\(-2\log\hat{L}\) 越小）。
  • \(k\) 是参数个数（模型越复杂，惩罚越大）。
  • \(n\) 是样本量；BIC 对复杂度的惩罚更强，因此更偏向“更简单的模型”。

对金融预测来说，最终还是要回到样本外：AIC/BIC 适合做“初筛”，不能替代滚动预测评估。

3.4 实证案例：宁波银行股票收益率预测

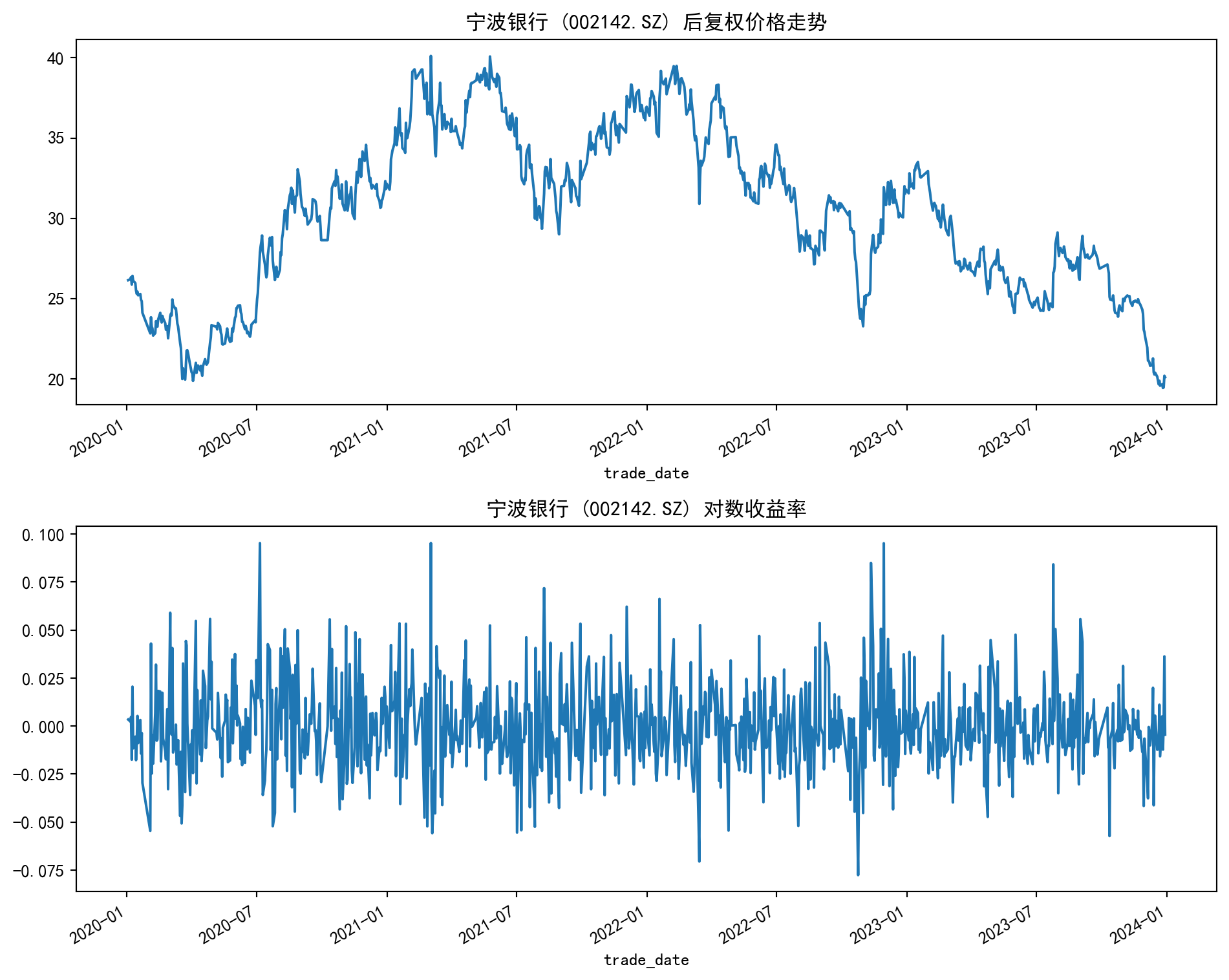
本节我们将选取宁波银行（002142.SZ），利用本项目的本地数据快照获取其历史交易数据（快照原始来源可为 Tushare/RQSDK），并构建ARIMA模型对其收益率进行拟合与预测。宁波银行作为城市商业银行的标杆，其股价表现反映了区域经济活力和小微企业融资环境。

3.4.1 数据获取与预处理

首先，我们从本地数据快照提取宁波银行 2020 年至今的日线数据，并计算对数收益率。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller
from pathlib import Path

plt.rcParams['font.family'] = ['Source Han Serif SC', 'SimHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False

df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))

# 1. 获取数据：宁波银行 (002142.SZ)
df = (df_all[df_all['ts_code'].eq('002142.SZ')]
      .sort_values('trade_date')
      .set_index('trade_date')
      .loc['2020-01-01':'2023-12-31']
      .copy())

# 2. 计算对数收益率（使用后复权收盘价更稳健）
df['log_ret'] = np.log(df['adj_close'] / df['adj_close'].shift(1))
df = df.dropna(subset=['log_ret'])

print(df[['adj_close', 'log_ret']].head())

# 绘制价格与收益率图
fig, axes = plt.subplots(2, 1, figsize=(10, 8))
df['adj_close'].plot(ax=axes[0], title='宁波银行 (002142.SZ) 后复权价格走势')
df['log_ret'].plot(ax=axes[1], title='宁波银行 (002142.SZ) 对数收益率')
plt.tight_layout()
plt.show()
            adj_close   log_ret
trade_date                     
2020-01-03  26.151551  0.003431
2020-01-06  26.214243  0.002394
2020-01-07  26.339627  0.004772
2020-01-08  25.882870 -0.017493
2020-01-09  26.420231  0.020549

3.4.2 平稳性检验

在建模之前，必须验证序列的平稳性。我们分别对“收盘价”和“对数收益率”进行 ADF 检验。

# 3. 平稳性检验 (ADF Test)
def perform_adf_test(series, name):
    result = adfuller(series)
    print(f"\n[{name}] ADF Test Results:")
    print(f"ADF Statistic: {result[0]:.4f}")
    print(f"p-value: {result[1]:.4f}")
    print("Critical Values:")
    for key, value in result[4].items():
        print(f"\t{key}: {value:.4f}")
    
    if result[1] < 0.05:
        print("结论: 拒绝原假设，序列是平稳的。")
    else:
        print("结论: 接受原假设，序列是非平稳的（存在单位根）。")

# 检验价格序列（通常非平稳）
# 本项目快照使用后复权收盘价 adj_close；若你用的是其他数据源，请相应替换字段。
perform_adf_test(df['adj_close'], '后复权收盘价')

# 检验收益率序列（通常平稳）
perform_adf_test(df['log_ret'], "对数收益率")

[后复权收盘价] ADF Test Results:
ADF Statistic: -1.7118
p-value: 0.4250
Critical Values:
    1%: -3.4372
    5%: -2.8645
    10%: -2.5684
结论: 接受原假设，序列是非平稳的（存在单位根）。

[对数收益率] ADF Test Results:
ADF Statistic: -31.9696
p-value: 0.0000
Critical Values:
    1%: -3.4372
    5%: -2.8645
    10%: -2.5684
结论: 拒绝原假设，序列是平稳的。

通常情况下，收盘价序列是非平稳的，而对数收益率序列是平稳的，这符合金融时间序列的一般特征。

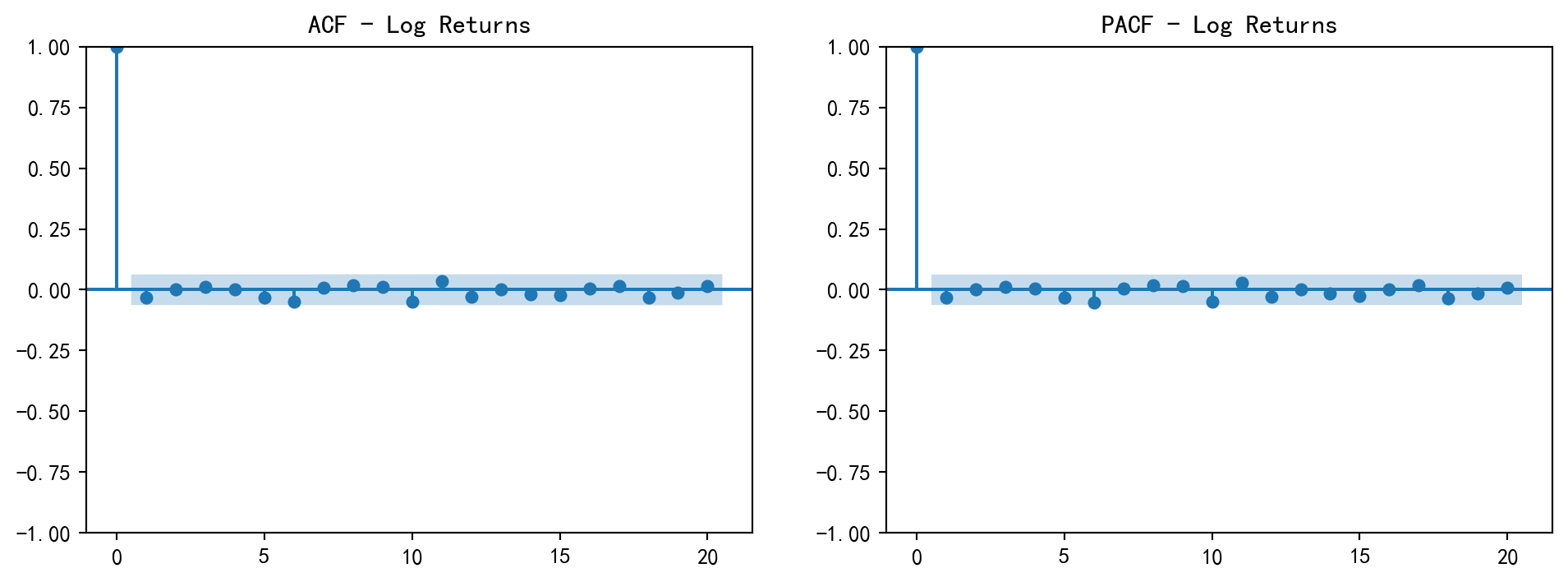
3.4.3 模型识别 (ACF/PACF)

确定序列平稳后（或进行差分后），我们需要通过自相关函数（ACF）和偏自相关函数（PACF）图来确定模型阶数 \(p\) 和 \(q\)。

  • ACF (AutoCorrelation Function)：用于判断 MA(q) 的阶数（截尾性）。
  • PACF (Partial ACF)：用于判断 AR(p) 的阶数（截尾性）。
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

# 4. 绘制 ACF 和 PACF
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
plot_acf(df['log_ret'], lags=20, ax=axes[0], title='ACF - Log Returns')
plot_pacf(df['log_ret'], lags=20, ax=axes[1], title='PACF - Log Returns')
plt.show()

如果 ACF 和 PACF 都表现为拖尾，则说明可能需要 ARMA 模型。在实践中，我们常通过 AIC (Akaike Information Criterion) 或 BIC 准则自动选择最优阶数。

3.4.4 模型拟合与预测

假设根据信息准则，我们选择 ARIMA(1, 0, 1) 模型对收益率序列进行建模（即 ARMA(1,1)）。

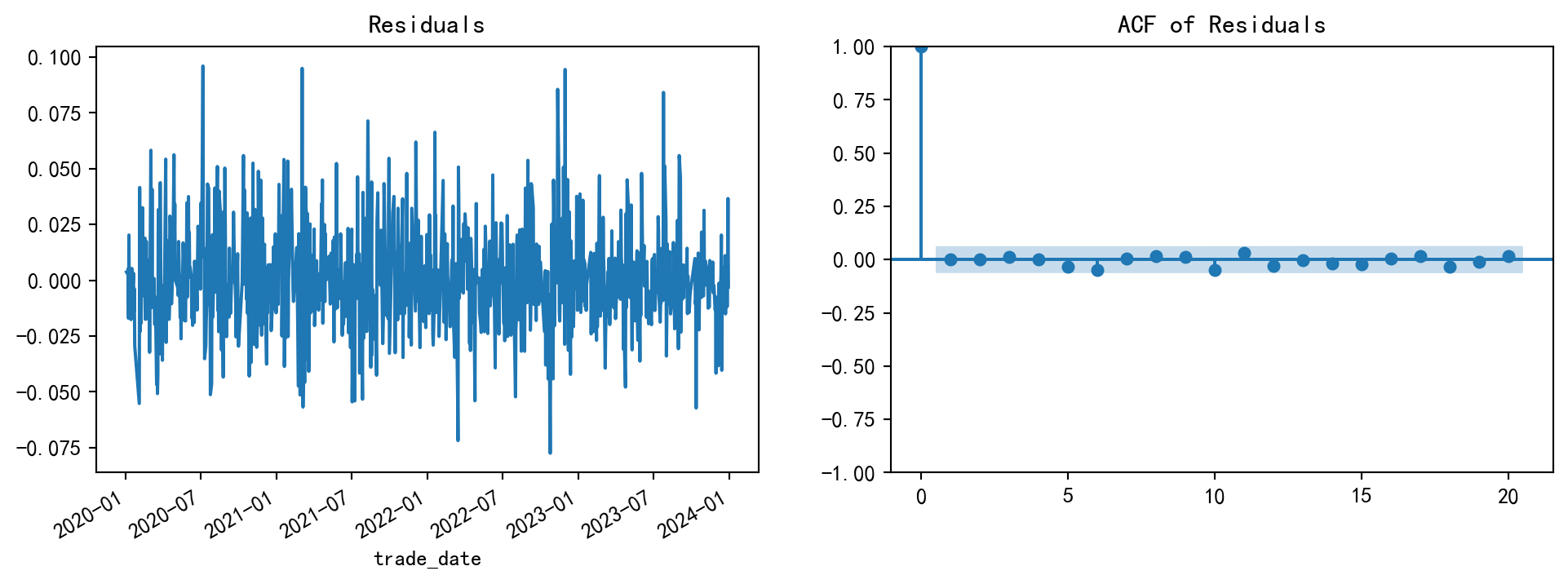
from statsmodels.tsa.arima.model import ARIMA

# 5. 拟合 ARIMA 模型
# 这里以 (p,d,q) = (1,0,1) 为例，实际应用中可用 pmdarima 进行自动定阶
model = ARIMA(df['log_ret'], order=(1, 0, 1))
model_fit = model.fit()

print(model_fit.summary())

# 6. 模型诊断：残差分析
residuals = model_fit.resid
fig, ax = plt.subplots(1, 2, figsize=(12, 4))
residuals.plot(title="Residuals", ax=ax[0])
plot_acf(residuals, lags=20, ax=ax[1], title="ACF of Residuals")
plt.show()

# 7. 预测未来一天的收益率
forecast_res = model_fit.get_forecast(steps=1)
pred_mean = forecast_res.predicted_mean.iloc[0]
conf_int = forecast_res.conf_int().iloc[0]

print(f"\n下一交易日收益率预测值: {pred_mean:.6f}")
print(f"95% 置信区间: [{conf_int.iloc[0]:.6f}, {conf_int.iloc[1]:.6f}]")
                               SARIMAX Results                                
==============================================================================
Dep. Variable:                log_ret   No. Observations:                  963
Model:                 ARIMA(1, 0, 1)   Log Likelihood                2299.965
Date:                Sun, 18 Jan 2026   AIC                          -4591.929
Time:                        22:25:16   BIC                          -4572.449
Sample:                             0   HQIC                         -4584.512
                                - 963                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const         -0.0003      0.001     -0.375      0.708      -0.002       0.001
ar.L1         -0.0640      0.970     -0.066      0.947      -1.965       1.837
ma.L1          0.0326      0.973      0.034      0.973      -1.874       1.939
sigma2         0.0005   1.78e-05     27.628      0.000       0.000       0.001
===================================================================================
Ljung-Box (L1) (Q):                   0.00   Jarque-Bera (JB):               132.61
Prob(Q):                              1.00   Prob(JB):                         0.00
Heteroskedasticity (H):               0.75   Skew:                             0.52
Prob(H) (two-sided):                  0.01   Kurtosis:                         4.49
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).


下一交易日收益率预测值: -0.000103
95% 置信区间: [-0.043626, 0.043420]

模型诊断是重要的一环，如果残差序列表现为白噪声（即 ACF 图中除了 0 阶外无显著非零值），则说明模型充分提取了数据中的信息。

提示

残差“像白噪声”到底怎么判断？（图 + 统计检验）

在课堂作业里，我们常用残差的 ACF 图做直观判断；在更严谨的实务里，你会配合一个整体检验，例如 Ljung–Box 检验。

  • 图形直觉：如果残差的 ACF 在多个滞后上仍显著偏离 0，说明模型遗漏了某些动态结构。
  • 统计检验（思想，不必死背公式）：Ljung–Box 把多个滞后阶的自相关“合并成一个统计量”，检验残差是否整体上存在自相关。
  • 与代码对应：本章在残差图旁边画了 plot_acf(residuals, ...)。如果你看到很多滞后点显著，你应该回到“模型识别/定阶”，而不是直接相信一步预测输出。

3.4.5 结果分析

通过上述分析，我们建立了一个基于历史数据的线性预测模型。需要注意的是，金融市场的有效市场假说（EMH）认为资产价格反映了所有公开信息，因此纯粹基于历史价格的线性模型（如 ARIMA）在实际预测股价涨跌时往往面临巨大的挑战，预测值的置信区间通常较宽。在后续章节中，我们将引入 GARCH 模型来处理波动率聚集现象，以更全面地描述金融时间序列的特征。

3.5 练习题

练习3.1：平稳性检验

对宁波银行(002142.SZ)与宁波港(601018.SH)分别检验：

  1. 后复权价格序列是否平稳？
  2. 对数收益率序列是否平稳？

给出 ADF 检验的统计量与 p 值，并用 5% 显著性水平解释结论。

练习3.2：ARIMA 阶数选择

以宁波银行对数收益率为例，在一个小网格中比较 (p, q) 的 AIC（例如 p,q ∈ {0,1,2}），并报告 AIC 最小的模型。

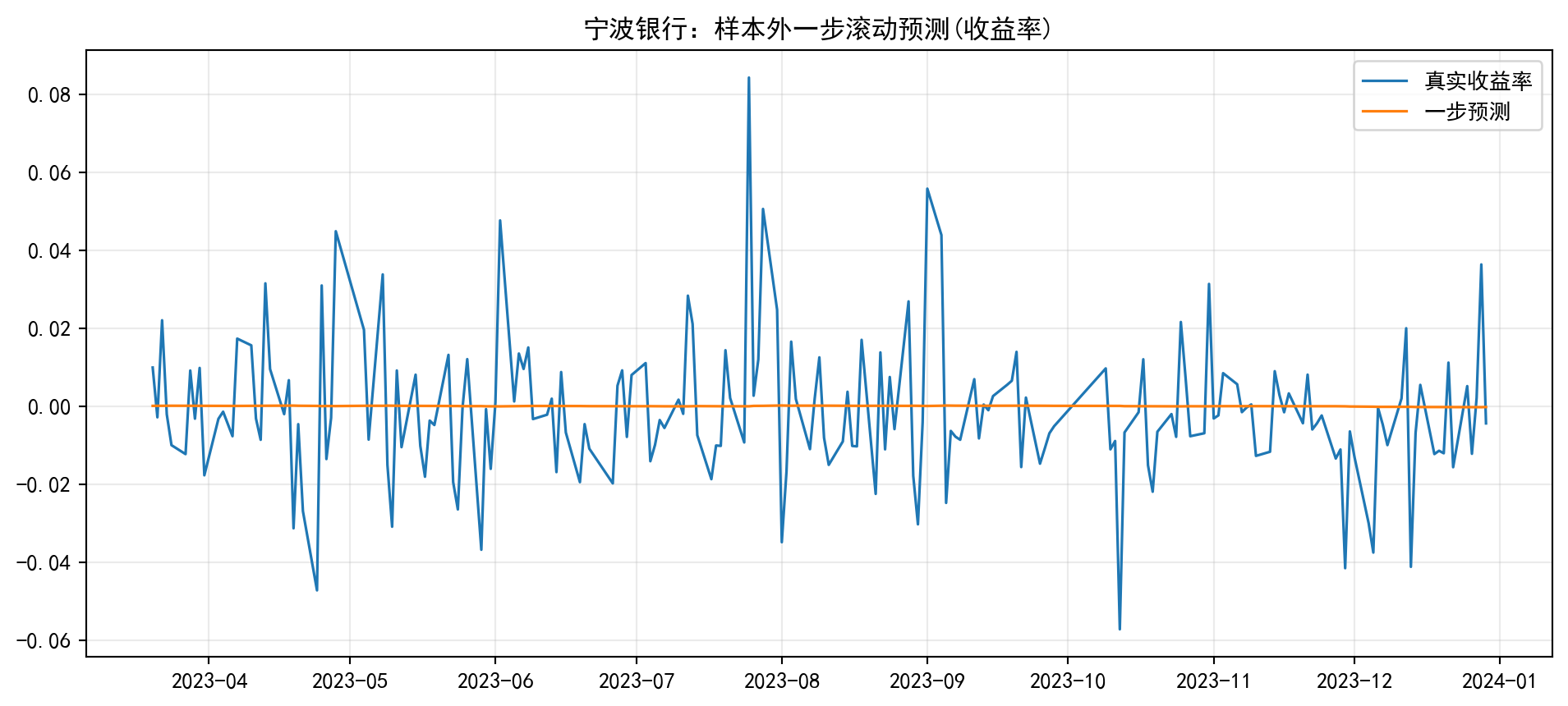
练习3.3：样本外预测评估

按时间顺序将样本切分为训练集（前 80%）与测试集（后 20%）。用训练集拟合 ARIMA，并对测试集做一步滚动预测（walk-forward），计算 MAE。

3.6 练习题完整解答

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.arima.model import ARIMA

plt.rcParams['font.family'] = ['Source Han Serif SC', 'SimHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False

df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))

def get_series(ts_code: str, col: str) -> pd.Series:
    df = (df_all[df_all['ts_code'].eq(ts_code)]
          .sort_values('trade_date')
          .set_index('trade_date')
          .loc['2020-01-01':'2023-12-31'])
    if col == 'log_ret':
        s = np.log(df['adj_close'] / df['adj_close'].shift(1))
        return s.dropna()
    return df[col].dropna()

def adf(series: pd.Series) -> tuple[float, float]:
    stat, pval, *_ = adfuller(series, autolag='AIC')
    return float(stat), float(pval)

# 练习3.1
for code, name in [('002142.SZ','宁波银行'), ('601018.SH','宁波港')]:
    price = get_series(code, 'adj_close')
    ret = get_series(code, 'log_ret')
    s1, p1 = adf(price)
    s2, p2 = adf(ret)
    print(f'[{name}] 价格 ADF={s1:.3f}, p={p1:.4f}；收益率 ADF={s2:.3f}, p={p2:.4f}')

# 练习3.2：小网格 AIC
y = get_series('002142.SZ', 'log_ret')
best = None
for p in [0,1,2]:
    for q in [0,1,2]:
        try:
            model = ARIMA(y, order=(p,0,q)).fit()
            aic = float(model.aic)
            if best is None or aic < best[0]:
                best = (aic, p, q)
        except Exception:
            continue
print(f'最佳 AIC={best[0]:.2f} 对应 ARIMA({best[1]},0,{best[2]})')

# 练习3.3：按时间顺序的样本外滚动预测
split = int(len(y) * 0.8)
train, test = y.iloc[:split], y.iloc[split:]

history = list(train.values)
preds = []
for t in range(len(test)):
    model = ARIMA(history, order=(best[1],0,best[2])).fit()
    yhat = float(model.forecast(steps=1)[0])
    preds.append(yhat)
    history.append(float(test.iloc[t]))

preds = pd.Series(preds, index=test.index)
mae = float(np.mean(np.abs(preds - test)))
print(f'样本外 MAE: {mae:.6f}')

plt.figure(figsize=(12, 5))
plt.plot(test.index, test.values, label='真实收益率', linewidth=1.2)
plt.plot(preds.index, preds.values, label='一步预测', linewidth=1.2)
plt.title('宁波银行：样本外一步滚动预测(收益率)')
plt.legend()
plt.grid(True, alpha=0.25)
plt.show()
[宁波银行] 价格 ADF=-1.716, p=0.4230；收益率 ADF=-31.970, p=0.0000
[宁波港] 价格 ADF=-3.146, p=0.0233；收益率 ADF=-15.972, p=0.0000
最佳 AIC=-4594.98 对应 ARIMA(0,0,0)
样本外 MAE: 0.013013

Box, George E. P., Gwilym M. Jenkins, Gregory C. Reinsel, 和 Greta M. Ljung. 2015. Time Series Analysis: Forecasting and Control. 5 本. Wiley. https://www.wiley.com/en-us/Time+Series+Analysis%3A+Forecasting+and+Control%2C+5th+Edition-p-9781118674925.