6  金融机器学习应用

随着大数据时代的到来，机器学习（Machine Learning, ML）已成为金融工程领域不可或缺的工具。与传统的计量经济学侧重于参数估计和因果推断不同，金融机器学习的核心目标在于预测（Prediction），尤其是样本外（Out-of-Sample）的泛化能力。本章将探讨机器学习在金融领域的应用范式、标准工作流，并以宁波地区的代表性金融机构为例，演示如何使用随机森林算法预测股价涨跌。

注记

机器学习在金融中的理论起源

金融机器学习的现代应用可追溯到两条主线：

  1. 算法层面：随机森林由 Breiman 系统提出，是金融分类/回归预测中最常用的非线性基线模型之一（Breiman (2001)）。
  2. 理论体系层面：统计学习框架（偏差-方差权衡、正则化、交叉验证）在经典教材中得到系统化阐述（Hastie, Tibshirani, 和 Friedman (2009)），为金融预测中的模型选择提供方法论基础。

最新发展: - 深度学习在高频交易中的应用 (LSTM, Transformer) - 强化学习在组合管理中的应用 - 图神经网络 (GNN) 在系统性风险分析中的应用

6.1 金融中的机器学习范式

在传统金融计量学中，我们通常寻找具有显著统计学意义的线性关系，关注 \(R^2\) 和 t 统计量。然而，金融市场充满了非线性、高噪音和动态变化的特征。机器学习范式在以下几个方面与传统方法存在显著差异：

  1. 目标导向：从“解释变异（In-sample Fit）”转向“样本外预测（Out-of-Sample Prediction）”。一个模型可能在历史数据上拟合极佳，但如果无法预测未来，在量化投资中则毫无价值。
  2. 数据驱动：减少对先验经济理论的依赖，更多地让数据通过算法“说话”，发现潜在的非线性模式。
  3. 过拟合风险（Overfitting）：这是金融ML面临的最大挑战。由于金融数据的信噪比（Signal-to-Noise Ratio）极低，复杂的模型极易学习到历史噪音而非真实规律。因此，正则化（Regularization）和严格的交叉验证（Cross-Validation）至关重要。
注记

偏差-方差权衡：用一句公式抓住过拟合的本质

把“预测误差”拆成三块（理解即可，不必背诵推导）： \[\mathbb{E}[(y-\hat{f}(x))^2] = \text{Bias}^2 + \text{Variance} + \sigma^2\]

  • 偏差（Bias）：模型太简单，学不到规律（欠拟合）。
  • 方差（Variance）：模型太灵活，对训练样本非常敏感（过拟合）。
  • \(\sigma^2\)：不可避免的噪声（金融里往往很大）。

与代码对应：随机森林通过“多棵树投票/平均”降低单棵树的方差（Bagging 思想），因此常被用作金融预测的稳健基线。

6.2 机器学习工作流

构建一个稳健的金融机器学习模型，需要遵循严格的工程化流程。不同于一般的图像识别或自然语言处理，金融时间序列数据具有序列相关性，处理不当极易导致“前视偏差（Look-ahead Bias）”。

典型的金融机器学习工作流如下：

数据获取 标签生成 特征工程 时序切分 训练与评估 严禁随机打乱！
图 6.1: 金融机器学习标准工作流
注意

数据泄漏（Look-ahead Bias）怎么发生？金融里最常见的 3 种“踩坑”

你只要记住一个原则：训练阶段能看到的信息，必须严格早于预测目标的时点。

  1. 用未来数据算特征：例如用全样本均值/方差做标准化，或用包含未来的窗口计算技术指标。
  2. 随机打乱时间序列：把未来样本混进训练集，会让评估指标虚高。
  3. 标签对齐错误：特征在 \(t\) 时点，标签却误用同一天或更早的涨跌（应明确预测 \(t+1\)、\(t+5\) 等）。

与代码对应：本章强调“时序切分”，并在后续的时序交叉验证中沿用这一原则。

  1. 数据获取与清洗：处理缺失值、离群点。
  2. 标签生成（Labeling）：定义预测目标。例如，\(y_{t+1} = 1\) 如果 \(r_{t+1} > 0\)，否则为 0。
  3. 特征工程（Feature Engineering）：挖掘预测因子，如滞后收益率、技术指标、宏观经济变量等。
  4. 时序切分（Time Series Split）：关键步骤。金融数据严禁使用传统的随机打乱（Shuffle）进行训练集和测试集划分，必须严格按照时间顺序，训练集在时间上必须先于测试集。
  5. 模型训练与评估：选择模型，调整超参数，使用准确率（Accuracy）、精确率（Precision）、召回率（Recall）等指标评估。
提示

标准化/归一化：只在训练集上‘学参数’，再应用到测试集

如果你对特征做 \(z\)-score 标准化： \[z = \frac{x-\mu}{\sigma}\] 那么 \(\mu,\sigma\) 必须只用训练集估计得到，再用于变换训练集与测试集；否则就会把测试集的信息“泄漏”回训练集。

与代码对应：当你在后文使用 StandardScaler 或类似步骤时，务必把 fit 放在训练集，transform 放在训练/测试集。

6.3 算法原理：随机森林

随机森林（Random Forest）是一种基于集成学习（Ensemble Learning）的算法，它通过构建多棵决策树（Decision Tree）并将结果进行汇总（分类问题取众数，回归问题取平均）来提高预测精度并控制过拟合。

6.3.1 决策树与基尼不纯度

决策树通过一系列规则将某些特征空间划分为矩形区域。在分类问题中，分裂的标准通常是基尼不纯度（Gini Impurity）。

假设一个节点包含 \(C\) 个类别，样本属于第 \(i\) 类的概率为 \(p_i\)，则该节点的基尼不纯度 \(G\) 定义为：

\[ G = \sum_{i=1}^C p_i (1 - p_i) = 1 - \sum_{i=1}^C p_i^2 \tag{6.1}\]

基尼不纯度越低，节点的纯度越高。决策树在每次分裂时，都会尝试最小化加权后的基尼不纯度。

提示

基尼不纯度的直观解释

基尼不纯度可以理解为”随机选取两个样本属于不同类别的概率”。

数学推导: 假设从节点中随机选取两个样本,它们属于不同类别的概率为: \[P(\text{不同类}) = \sum_{i=1}^{C}\sum_{j\neq i} p_i p_j = \sum_{i=1}^{C} p_i(1-p_i)\]

极端情况: - 当所有样本属于同一类时: \(G=0\) (完美纯度) - 当样本均匀分布于\(C\)个类时: \(G=1-\frac{1}{C}\) (最大不纯度)

6.3.2 Bagging (Bootstrap Aggregating)

为了解决单棵决策树容易过拟合的问题，随机森林引入了 Bagging 技术： 1. 自助采样（Bootstrap Sampling）：从原始训练集中有放回地随机抽取样本，生成多个训练子集。 2. 随机特征选择：在构建每棵树的每个节点分裂时，只随机考虑一小部分特征。

这种双重随机性（行随机和列随机）极大地降低了模型方差。

6.4 案例研究：预测宁波银行（002142.SZ）股价涨跌

我们将使用随机森林模型预测宁波银行的涨跌。作为城市商业银行的标杆，宁波银行的股价走势反映了区域经济的景气度和小微企业融资环境。

本案例将直接使用宁波银行（002142.SZ）的历史数据，构建一个二分类模型，预测下一交易日的股价是否会上涨。

6.4.1 数据获取与特征工程

我们将从本项目的本地数据快照（data/cn_equity_daily_latest.parquet）读取行情数据。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

plt.style.use('seaborn-v0_8')
plt.rcParams['font.sans-serif'] = ['Source Han Serif SC', 'SimHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False

# 1. 读取宁波银行 (002142.SZ) 的日线数据（本地快照）
df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))
df = (df_all[df_all['ts_code'].eq('002142.SZ')]
  .sort_values('trade_date')
  .set_index('trade_date')
  .loc['2018-01-01':'2023-12-31']
  .copy())
df.index = pd.to_datetime(df.index)

# 使用后复权收盘价构造特征（更稳健）
df['price'] = df['adj_close']

# 2. 特征工程
# 计算对数收益率
df['log_ret'] = np.log(df['price'] / df['price'].shift(1))

# 特征 1-3: 滞后收益率 (Lagged Returns)
# 昨天的涨跌、前天的涨跌很可能通过动量或反转效应影响今天
df['lag_1'] = df['log_ret'].shift(1)
df['lag_2'] = df['log_ret'].shift(2)
df['lag_5'] = df['log_ret'].shift(5)

# 特征 4-5: 移动平均线 (Moving Averages) 偏离度
# 价格相对于均线的位置
df['ma_5'] = df['price'] / df['price'].rolling(window=5).mean() - 1
df['ma_20'] = df['price'] / df['price'].rolling(window=20).mean() - 1

# 特征 6: 波动率 (Volatility)
# 过去20天的波动率
df['vol_20'] = df['log_ret'].rolling(window=20).std()

# 3. 标签生成 (Labeling)
# 目标：预测 *下一天* 的收益率为正 (1) 还是非正 (0)
# 注意：我们必须使用 shift(-1) 将未来的收益对齐到当天的特征上
df['target'] = np.where(df['log_ret'].shift(-1) > 0, 1, 0)

# 删除包含 NaN 的行 (由于 shift 和 rolling 操作产生)
df_model = df.dropna()

print(f"数据总样本数: {len(df_model)}")
df_model[['price', 'log_ret', 'target']].tail()
数据总样本数: 1431
price log_ret target
trade_date
2023-12-25 19.68 0.005094 0
2023-12-26 19.44 -0.012270 1
2023-12-27 19.48 0.002055 1
2023-12-28 20.20 0.036294 0
2023-12-29 20.11 -0.004465 0

6.4.2 模型训练与评估（时序交叉验证）

在金融数据中，简单的 train_test_split 随机划分是错误的，因为它会引入未来的信息。我们手动将数据按时间切分：前 80% 用于训练，后 20% 用于测试。

注记

混淆矩阵是什么？为什么金融预测一定要看它？

对二分类问题（例如“未来5日上涨/下跌”），混淆矩阵把预测结果按四种情况分组：

  • TP (True Positive)：真实上涨，模型也预测上涨。
  • FP (False Positive)：真实下跌，但模型预测上涨（可能导致‘追涨’误判）。
  • TN (True Negative)：真实下跌，模型也预测下跌。
  • FN (False Negative)：真实上涨，但模型预测下跌（可能错过机会）。

基于这四项，我们才能计算更有解释力的指标（比单纯准确率更稳健）：

\[ ext{Precision} = \frac{TP}{TP + FP},\quad ext{Recall} = \frac{TP}{TP + FN},\quad F_1 = \frac{2\cdot \text{Precision}\cdot \text{Recall}}{\text{Precision}+\text{Recall}} \]

在金融场景中，类别分布常常不平衡（例如上涨天数略多/略少），此时只看 Accuracy 可能会产生误导；混淆矩阵能帮助你判断错误主要来自哪一类，从而决定是调阈值、换损失函数，还是回到特征工程。

# 准备特征矩阵 X 和 目标向量 y
feature_cols = ['lag_1', 'lag_2', 'lag_5', 'ma_5', 'ma_20', 'vol_20']
X = df_model[feature_cols]
y = df_model['target']

# 严格按时间切分
split_point = int(len(X) * 0.8)
X_train, X_test = X.iloc[:split_point], X.iloc[split_point:]
y_train, y_test = y.iloc[:split_point], y.iloc[split_point:]

print(f'训练集区间: {X_train.index.min().date()} 至 {X_train.index.max().date()}')
print(f'测试集区间: {X_test.index.min().date()} 至 {X_test.index.max().date()}')

# 初始化随机森林分类器
# n_estimators: 树的数量
# max_depth: 树的深度，防止过拟合
# random_state: 保证结果可复现
rf_clf = RandomForestClassifier(n_estimators=100, max_depth=5, min_samples_leaf=10, random_state=42, n_jobs=-1)

# 训练模型
rf_clf.fit(X_train, y_train)

# 预测
y_pred = rf_clf.predict(X_test)

# 评估
acc = accuracy_score(y_test, y_pred)
print(f'\n测试集准确率 (Accuracy): {acc:.4f}')

# 混淆矩阵
cm = confusion_matrix(y_test, y_pred)
print('\n混淆矩阵:')
print(cm)
print('\n分类报告:')
print(classification_report(y_test, y_pred))
训练集区间: 2018-01-30 至 2022-10-28
测试集区间: 2022-10-31 至 2023-12-29

测试集准确率 (Accuracy): 0.5366

混淆矩阵:
[[112  61]
 [ 72  42]]

分类报告:
              precision    recall  f1-score   support

           0       0.61      0.65      0.63       173
           1       0.41      0.37      0.39       114

    accuracy                           0.54       287
   macro avg       0.51      0.51      0.51       287
weighted avg       0.53      0.54      0.53       287

注：金融市场的预测准确率通常略高于 50% 即可产生超额收益，因为交易成本和风险管理同样重要。此处仅为演示；实际落地通常需要更丰富的特征、更稳定的验证框架，以及对交易成本/滑点的显式建模。

6.5 模型可解释性

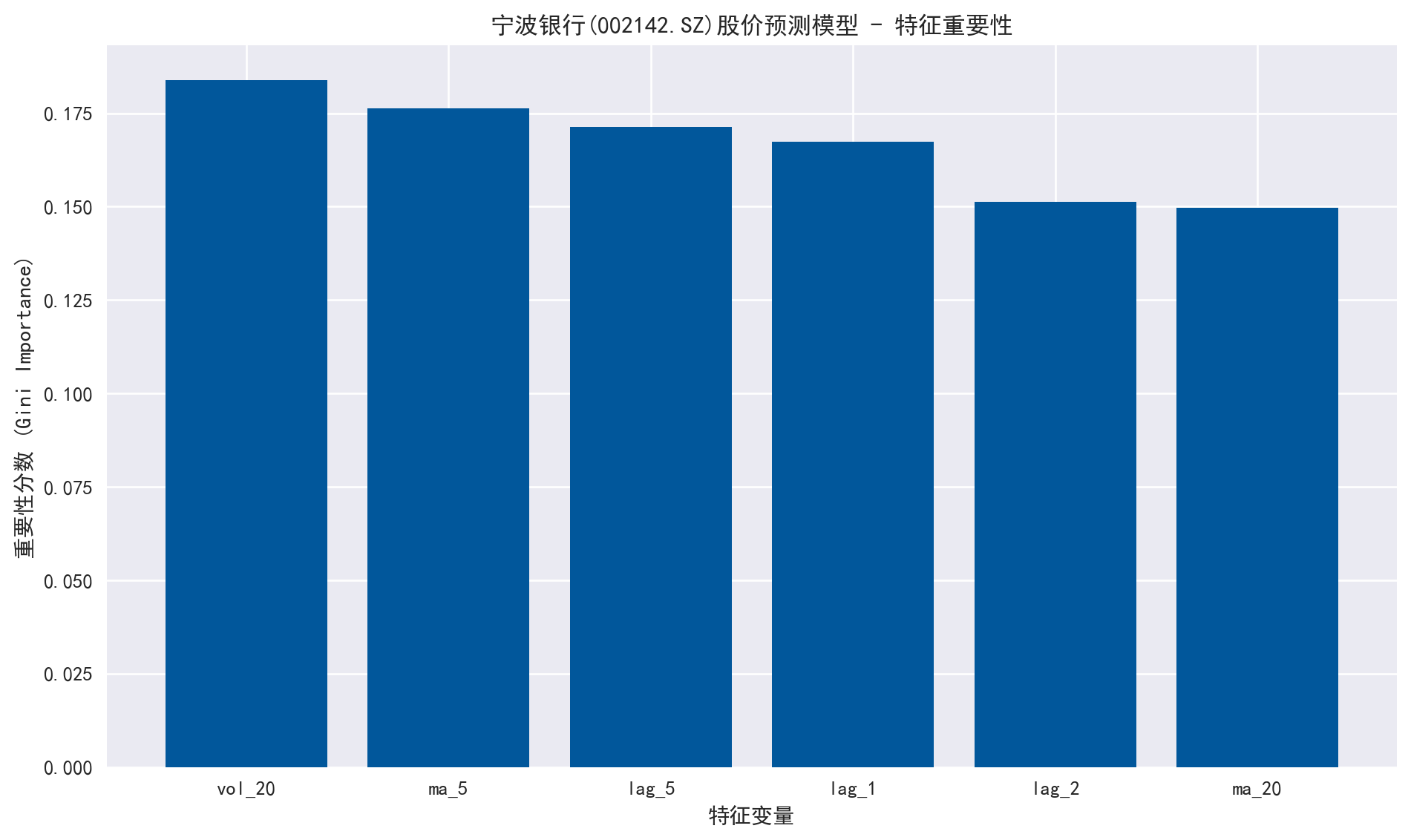
随机森林的一个优点是可以输出特征重要性（Feature Importance），帮助我们理解哪些因子对预测宁波银行的股价更有效。

# 提取特征重要性
importances = rf_clf.feature_importances_
indices = np.argsort(importances)[::-1]

# 绘图
plt.figure(figsize=(10, 6))
plt.title('宁波银行(002142.SZ)股价预测模型 - 特征重要性')
plt.bar(range(X.shape[1]), importances[indices], align='center', color='#01579b')
plt.xticks(range(X.shape[1]), [feature_cols[i] for i in indices])
plt.xlabel('特征变量')
plt.ylabel('重要性分数 (Gini Importance)')
plt.tight_layout()
plt.show()

6.6 练习题

练习6.1：增加基准模型并比较

在相同的特征工程与时序切分下，使用逻辑回归（Logistic Regression）作为基准模型，与随机森林比较测试集准确率，并讨论两者差异可能来自哪里（模型偏差/方差、非线性拟合能力等）。

练习6.2：滚动评估（Walk-forward）

使用扩展窗口（Expanding Window）的方式做 5 折滚动评估：每一折用过去数据训练，用下一段时间测试，报告每折的准确率均值与标准差。

6.7 练习题完整解答

import pandas as pd
import numpy as np
from pathlib import Path
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))
df = (df_all[df_all['ts_code'].eq('002142.SZ')]
    .sort_values('trade_date')
    .set_index('trade_date')
    .loc['2018-01-01':'2023-12-31']
    .copy())
df.index = pd.to_datetime(df.index)
df['price'] = df['adj_close']
df['log_ret'] = np.log(df['price'] / df['price'].shift(1))
df['lag_1'] = df['log_ret'].shift(1)
df['lag_2'] = df['log_ret'].shift(2)
df['lag_5'] = df['log_ret'].shift(5)
df['ma_5'] = df['price'] / df['price'].rolling(5).mean() - 1
df['ma_20'] = df['price'] / df['price'].rolling(20).mean() - 1
df['vol_20'] = df['log_ret'].rolling(20).std()
df['target'] = (df['log_ret'].shift(-1) > 0).astype(int)
dfm = df.dropna()

feature_cols = ['lag_1', 'lag_2', 'lag_5', 'ma_5', 'ma_20', 'vol_20']
X = dfm[feature_cols]
y = dfm['target']

split_point = int(len(X) * 0.8)
X_train, X_test = X.iloc[:split_point], X.iloc[split_point:]
y_train, y_test = y.iloc[:split_point], y.iloc[split_point:]

# 练习6.1：逻辑回归基准 vs 随机森林
lr = LogisticRegression(max_iter=2000)
lr.fit(X_train, y_train)
pred_lr = lr.predict(X_test)
acc_lr = accuracy_score(y_test, pred_lr)

rf = RandomForestClassifier(n_estimators=200, max_depth=6, min_samples_leaf=10, random_state=42, n_jobs=-1)
rf.fit(X_train, y_train)
pred_rf = rf.predict(X_test)
acc_rf = accuracy_score(y_test, pred_rf)

print({'acc_logit': float(acc_lr), 'acc_rf': float(acc_rf)})

# 练习6.2：扩展窗口滚动评估（5 折；最小计算用时示范）
folds = 5
cut_points = np.linspace(0.6, 0.9, folds)  # 训练集终点占比（示范）
accs = []
for frac in cut_points:
    train_end = int(len(X) * frac)
    test_end = min(train_end + int(len(X) * 0.1), len(X))
    X_tr, y_tr = X.iloc[:train_end], y.iloc[:train_end]
    X_te, y_te = X.iloc[train_end:test_end], y.iloc[train_end:test_end]
    if len(X_te) < 50:
        continue
    m = RandomForestClassifier(n_estimators=200, max_depth=6, min_samples_leaf=10, random_state=42, n_jobs=-1)
    m.fit(X_tr, y_tr)
    accs.append(accuracy_score(y_te, m.predict(X_te)))

accs = np.array(accs)
print({'walk_forward_acc_mean': float(accs.mean()), 'walk_forward_acc_std': float(accs.std(ddof=1)), 'n_folds_used': int(len(accs))})
{'acc_logit': 0.6062717770034843, 'acc_rf': 0.5331010452961672}
{'walk_forward_acc_mean': 0.5258741258741259, 'walk_forward_acc_std': 0.025406856118300625, 'n_folds_used': 5}

上图展示了各特征对模型预测能力的贡献度。通常，波动率（Volatility）和短期动量（Lagged Returns）在短期价格预测中扮演重要角色。通过分析特征重要性，分析师可以进一步优化因子库，剔除噪音特征。

Breiman, Leo. 2001. 《Random Forests》. Machine Learning 45 (1): 5–32. https://doi.org/10.1023/A:1010933404324.
Hastie, Trevor, Robert Tibshirani, 和 Jerome Friedman. 2009. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2 本. Springer. https://doi.org/10.1007/978-0-387-84858-7.