2  金融数据处理与分析

金融工程的核心在于将数学模型应用于金融数据，以发现市场规律、管理风险或构建投资策略。然而，现实世界中的金融数据往往是“脏”的：存在缺失值、异常值、格式不统一等问题。如果在分析之前没有经过严谨的处理流程，那么再复杂的模型也只能得出无意义的结论，正所谓“垃圾进，垃圾出”(Garbage In, Garbage Out)。

本章将深入探讨如何使用Python的Pandas库构建专业的金融数据处理流水线。我们将重点关注宁波港(601018.SH)和宁波银行(002142.SZ)这两家宁波地区代表企业的数据,通过实战案例演示数据的获取、清洗、对齐以及特征工程。

2.1 理论基础:金融时间序列的数学性质

2.1.1 时间序列的随机过程表示

注记

金融时间序列理论起源

金融时间序列分析的现代理论起源于Louis Bachelier 1900年的博士论文《投机理论》(Bachelier 1900),他首次将布朗运动应用于股价建模。这一开创性工作比爱因斯坦关于布朗运动的论文早了5年,但直到1960年代Paul Samuelson重新发现后才被广泛认可(Samuelson 1965)。

最新发展包括: - 分形市场假说(Mandelbrot 和 Hudson 2013): 挑战传统有效市场假说,认为市场具有长记忆性 - 高频交易微观结构(Hasbrouck 2007): 研究毫秒级价格形成机制 - 机器学习时序建模(Dixon, Halperin, 和 Bilokon 2020): LSTM、Transformer等深度学习在价格预测中的应用

参考文献: 1. Bachelier, L. (1900). Théorie de la spéculation. Annales scientifiques de l’École normale supérieure, 17, 21-86. URL: http://www.numdam.org/item/ASENS_1900_3_17__21_0/

  1. Tsay, R. S. (2010). Analysis of Financial Time Series. John Wiley & Sons. DOI: https://doi.org/10.1002/9780470644560

  2. Campbell, J. Y., Lo, A. W., & MacKinlay, A. C. (1997). The Econometrics of Financial Markets. Princeton University Press. DOI: https://doi.org/10.1515/9781400830213

一个金融资产的价格过程\(\{P_t\}_{t \geq 0}\)可以表示为随机过程。在连续时间框架下,最基本的模型是几何布朗运动:

\[ dP_t = \mu P_t dt + \sigma P_t dW_t \tag{2.1}\]

其中\(\mu\)是漂移率(drift),\(\sigma\)是波动率(volatility),\(W_t\)是标准布朗运动。

提示

完整推导:从离散到连续

从离散时间的对数收益率出发: \[ r_t = \ln(P_t) - \ln(P_{t-1}) \]

假设\(r_t \sim N(\mu \Delta t, \sigma^2 \Delta t)\),当\(\Delta t \to 0\)时,根据伊藤引理(Itô’s Lemma): \[ d\ln(P_t) = (\mu - \frac{\sigma^2}{2})dt + \sigma dW_t \]

对上式应用指数函数即得到@eq-gbm。这一推导过程的严格性需要测度论基础,但直观理解是:价格的随机变化可以分解为确定性趋势项和随机扰动项。

实际意义: - \(\mu\): 资产的预期收益率 - \(\sigma\): 收益率的标准差(风险度量) - 该模型是Black-Scholes期权定价公式的基础

2.1.2 平稳性与协整性

在实际应用中,价格序列\(\{P_t\}\)通常是非平稳的(non-stationary),但其对数收益率\(\{r_t\}\)往往是平稳的(stationary)。平稳性是许多统计推断的前提条件。

弱平稳性定义: 若时间序列\(\{X_t\}\)满足: 1. \(E[X_t] = \mu\) (常数均值) 2. \(Var(X_t) = \sigma^2 < \infty\) (有限方差) 3. \(Cov(X_t, X_{t+k}) = \gamma_k\) (自协方差只依赖于滞后期\(k\))

则称其为弱平稳序列。

2.2 数据清洗流程

在进行任何定量分析之前，建立一个标准化的数据处理流水线（Pipeline）是至关重要的。一个典型的数据流水线包含原始数据获取、清洗（处理缺失与异常）、转换（特征提取）以及最终的分析建模。

以下是金融数据处理的标准流水线示意图：

原始数据获取 scripts/ → data/ API / CSV / 数据库 数据清洗 缺失值 / 异常值 交易日对齐 特征转换 收益率 / 波动率 重采样 / 滚动 分析与建模 回测 / 预测 / 归因 风险 / 投资组合 从‘可追溯的数据快照’出发，保证建模与结论可复现
图 2.1: 金融数据处理标准流水线

2.3 金融数据的 Pandas 高级处理

在 Python 生态中，Pandas 是处理结构化数据的绝对核心。对于金融时间序列数据，Pandas 提供了极其强大的索引和重采样功能。

2.3.1 数据的获取与索引设置

首先，我们从本项目的本地数据快照获取宁波港(601018.SH)的历史行情数据（快照原始来源可为 Tushare/RQSDK）。宁波港是全球第三大港口,也是长三角地区重要的物流枢纽,其股价走势与国际贸易景气度高度相关。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path

# 统一从本地数据快照读取（避免在正文中直连 API）
df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))

# 获取宁波港(601018.SH) 2022-2023 日线数据
df = (df_all[df_all['ts_code'].eq('601018.SH')]
      .sort_values('trade_date')
      .set_index('trade_date')
      .loc['2022-01-01':'2023-12-31']
      .copy())

# 设置中文字体
plt.rcParams['font.family'] = ['Source Han Serif SC', 'SimHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False

print(df[['close', 'volume']].head())
            close     volume
trade_date                  
2022-01-04   4.04  254832.00
2022-01-05   4.18  923561.37
2022-01-06   4.22  558410.25
2022-01-07   4.21  371114.13
2022-01-10   4.20  232232.98

2.3.2 收益率计算与数学定义

在金融分析中，我们通常关注收益率而非价格本身，因为收益率具有更好的统计性质（如平稳性）。

简单收益率 (Simple Return) 定义为： \[ R_t = \frac{P_t - P_{t-1}}{P_{t-1}} = \frac{P_t}{P_{t-1}} - 1 \]

对数收益率 (Log Return) 定义为： \[ r_t = \ln\left(\frac{P_t}{P_{t-1}}\right) = \ln(P_t) - \ln(P_{t-1}) \]

注记

简单收益率 vs 对数收益率：到底该用哪个？

两者都在实践中常用，但侧重点不同：

  • 可加性：对数收益率满足跨期相加的近似可加性：\(\ln(P_T/P_0)=\sum_{t=1}^T r_t\)，因此在做多期累计收益、回归或波动率建模时更方便。
  • 解释性：简单收益率更直观（涨了多少百分比），更贴近业务口径与报表表达。

常见误区是把两者混用：例如用对数收益率计算了日收益，却用简单收益率的方式去累计，导致结果出现细小但系统性的偏差。

Pandas 提供了 pct_change() 方法快速计算简单收益率：

# 计算日收益率
df['daily_return'] = df['close'].pct_change()

# 查看收益率统计特征
print(df['daily_return'].describe())
count    483.000000
mean      -0.000190
std        0.012035
min       -0.055416
25%       -0.005618
50%        0.000000
75%        0.005587
max        0.070755
Name: daily_return, dtype: float64

2.3.3 重采样 (Resampling) 与 滚动窗口 (Rolling)

高频数据往往包含大量噪声。为了捕捉长期趋势，我们常需要降低数据频率（例如将日线转换为月线），或使用移动平均线。

  1. 重采样 (resample): 类似于 SQL 中的 GROUP BY，但专门针对时间序列。
  2. 滚动窗口 (rolling): 用于计算移动平均、移动波动率等。
# 1. 重采样：将日线数据转换为月度数据，取每月的最后一个收盘价
monthly_close = df['close'].resample('M').last()

# 2. 滚动窗口：计算 20 日移动平均线 (MA20)
df['MA20'] = df['close'].rolling(window=20).mean()

# 3. 滚动波动率：计算 20 日滚动标准差（年化）
# 年化因子 sqrt(252)，假设一年有 252 个交易日
df['volatility_20d'] = df['daily_return'].rolling(window=20).std() * np.sqrt(252)

print(df[['close', 'MA20', 'volatility_20d']].tail())
            close    MA20  volatility_20d
trade_date                               
2023-12-25   3.60  3.6350        0.136438
2023-12-26   3.60  3.6345        0.134940
2023-12-27   3.61  3.6355        0.133721
2023-12-28   3.57  3.6335        0.138028
2023-12-29   3.56  3.6305        0.137682

\[ \sigma_{\text{annual}} \approx \sigma_{\text{daily}}\sqrt{252} \]

注意

年化的平方根法则：什么时候成立，什么时候会失真？

很多同学会记住‘年化波动率 = 日波动率 \(\times \sqrt{252}\)’，但忽略了它的统计前提。更准确地说，当收益率满足‘弱相关、方差稳定’等条件时，近似有：

见上式。

在以下情形里，上述平方根法则往往会偏离真实年化风险：

  • 波动率显著时变（例如危机期 vs 平稳期）
  • 收益率存在明显自相关或跳跃（高频、涨跌停机制、事件冲击）

因此，本书后续在 章节 4 的风险管理里会引入 GARCH 等模型，用‘条件波动率’来更贴近真实风险。

2.4 缺失值处理

在金融市场中，缺失值（Missing Data）非常常见，主要原因包括： 1. 非交易日：周末、法定节假日。 2. 停牌：公司因重大事项暂停交易。 3. 数据源错误：采集过程中的丢失。

2.4.1 dropna() vs fillna()

简单粗暴地删除缺失值 (dropna()) 往往不是最佳选择，因为它会破坏时间序列的连续性，特别是在计算滞后项（Lag）或计算多资产相关性时。

在金融领域，前向填充 (Forward Fill) 是最常用的处理方法。

  • 逻辑：如果今天没有数据（例如停牌），我们假设市场对该资产的估值保持在最后一次交易的价格水平。这一假设符合市场惯例。
import pandas as pd
from pathlib import Path

df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))

# 用真实数据构造“更完整的日历索引”，从而产生缺失值：
# - 周末/法定节假日：工作日日历里可能没有交易（缺失）
# - 上市前：例如中芯国际(688981.SH)在 2020 年才上市，2019 年将天然缺失
start, end = '2019-01-01', '2021-12-31'
calendar = pd.date_range(start, end, freq='B')  # 工作日日历（包含部分法定假日）

def close_series(ts_code: str) -> pd.Series:
    s = (df_all[df_all['ts_code'].eq(ts_code)]
         .sort_values('trade_date')
         .set_index('trade_date')['adj_close']
         .loc[start:end])
    return s.reindex(calendar)

panel = pd.DataFrame({
    '宁波港': close_series('601018.SH'),
    '宁波银行': close_series('002142.SZ'),
    '中芯国际': close_series('688981.SH'),
})

print('缺失值占比(示例日历):')
print(panel.isna().mean().sort_values(ascending=False))

# 常见做法：对“交易日缺口”做前向填充；但对“上市前缺口”不应填充（否则会引入伪数据）。
panel_ffill = panel.ffill()
print('前向填充后(前5行):')
print(panel_ffill.head())
缺失值占比(示例日历):
中芯国际    0.543367
宁波银行    0.076531
宁波港     0.068878
dtype: float64
前向填充后(前5行):
                 宁波港       宁波银行  中芯国际
2019-01-01       NaN        NaN   NaN
2019-01-02  2.964286  14.074821   NaN
2019-01-03  2.982143  14.171646   NaN
2019-01-04  3.035714  14.479726   NaN
2019-01-07  3.062500  14.567748   NaN

2.5 案例研究：宁波地区行业对比分析

为了综合运用上述技术,我们对宁波港(601018.SH)和宁波银行(002142.SZ)进行深入对比分析。这两家公司分别代表宁波地区的实体经济(港口物流)和金融服务业,具有很强的行业代表性。

研究意义: 1. 宁波港: 全球货物吞吐量第三大港,是”一带一路”海上丝绸之路的重要节点,其业绩反映国际贸易景气度 2. 宁波银行: 城市商业银行标杆,深耕长三角小微企业金融服务,是区域经济活力的晴雨表

通过对比分析,我们可以观察: - 不同行业对宏观经济周期的敏感性差异 - 金融与实体经济的联动关系 - 波动率特征与风险收益权衡

2.5.1 步骤 1：获取多只股票数据与对齐

不同股票可能因为各自的停牌事件导致时间轴不一致。Pandas 的 concat 或 merge 操作可以自动基于索引（日期）进行对齐。

# 统一从本地数据快照读取
from pathlib import Path
import pandas as pd

df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))

# 定义宁波地区代表性企业股票池
tickers = {
    '601018.SH': '宁波港',
    '002142.SZ': '宁波银行'
}

close_prices = pd.DataFrame()

for code, name in tickers.items():
    tmp_df = (df_all[df_all['ts_code'].eq(code)]
             .sort_values('trade_date')
             .set_index('trade_date')
             .loc['2023-01-01':'2023-12-31']
             .copy())

    # 提取后复权收盘价并改名
    close_prices[name] = tmp_df['adj_close']

# 按时间排序
close_prices.sort_index(inplace=True)

# 检查缺失值情况
print("缺失值数量：\n", close_prices.isnull().sum())

# 处理缺失值（如果有停牌，用前一交易日价格填充）
close_prices = close_prices.ffill()
缺失值数量：
 宁波港     0
宁波银行    0
dtype: int64

2.5.2 步骤 2：构建宁波地区经济指数

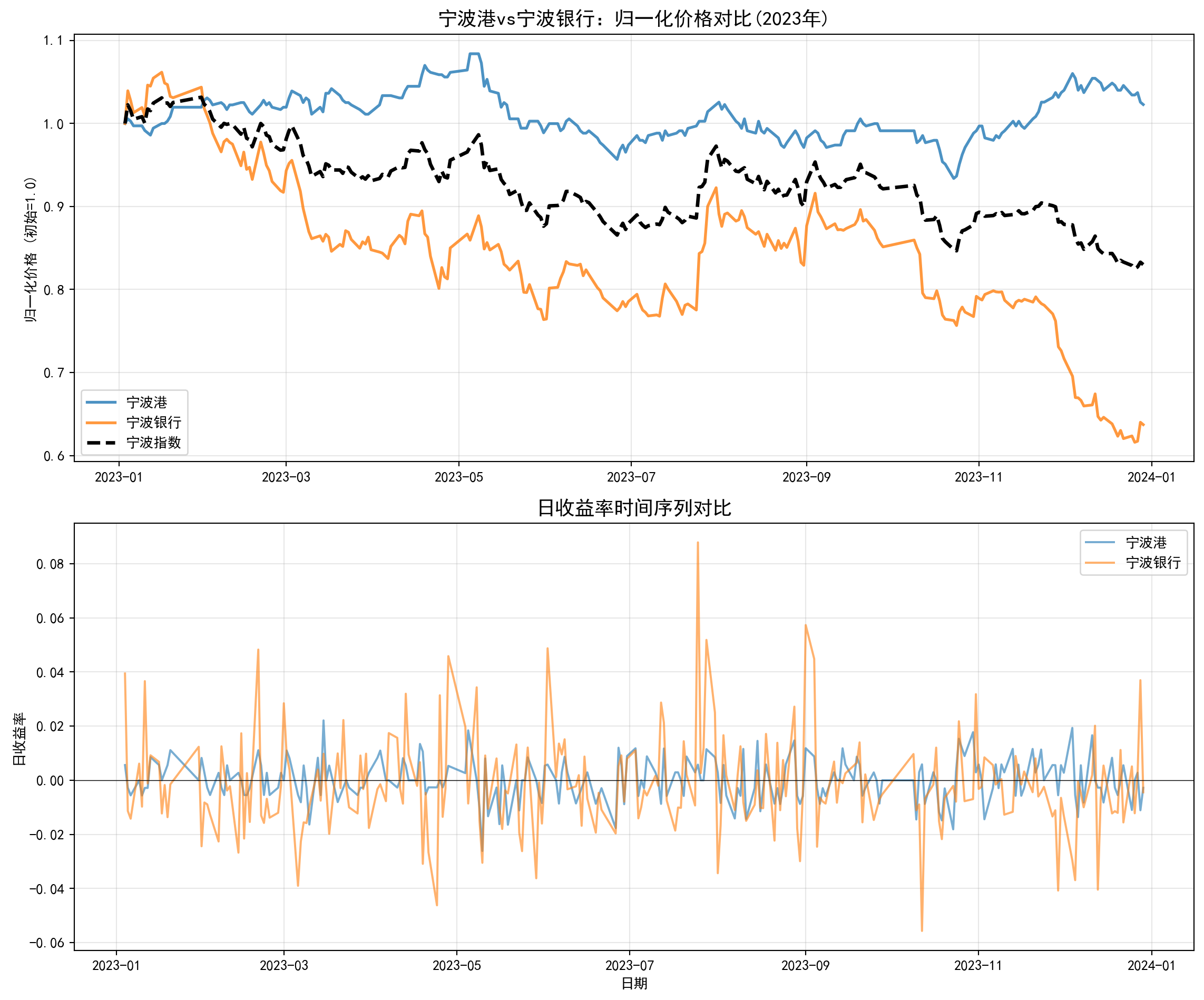
我们构建一个等权重指数(Equal-Weighted Index)来追踪宁波地区这两家代表企业的整体表现。将每只股票的价格归一化(以第一天为基准100),然后取平均值。

\[ I_t = 100 \times \frac{1}{N} \sum_{i=1}^{N} \frac{P_{i,t}}{P_{i,0}} \tag{2.2}\]

提示

等权重vs市值加权指数

上式（等权重指数定义）给予每只股票相同的权重 \(1/N\)。这与市值加权指数不同:

市值加权指数: \(I_t^{MW} = \sum_{i=1}^{N} w_i \frac{P_{i,t}}{P_{i,0}}\),其中\(w_i = \frac{MC_i}{\sum MC_i}\)

优劣对比: - 等权重指数更能反映”平均股票”的表现,适合行业对比 - 市值加权指数更接近市场实际投资,但易受大市值股票主导 - 学术研究表明,等权重指数长期表现往往优于市值加权(规模效应)

# 归一化：除以第一天的价格
normalized_prices = close_prices / close_prices.iloc[0]

# 计算等权重指数
ningbo_index = normalized_prices.mean(axis=1) * 100

# 绘制对比图
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10))

# 上图：归一化价格对比
for col in normalized_prices.columns:
    ax1.plot(normalized_prices.index, normalized_prices[col], label=col, linewidth=2, alpha=0.8)
ax1.plot(normalized_prices.index, ningbo_index/100, label='宁波指数', 
         linewidth=2.5, color='black', linestyle='--')
ax1.set_title('宁波港vs宁波银行：归一化价格对比(2023年)', fontsize=14, fontweight='bold')
ax1.set_ylabel('归一化价格 (初始=1.0)')
ax1.legend(loc='best')
ax1.grid(True, alpha=0.3)

# 下图：日收益率对比
returns = close_prices.pct_change()
for col in returns.columns:
    ax2.plot(returns.index, returns[col], label=col, alpha=0.6)
ax2.set_title('日收益率时间序列对比', fontsize=14, fontweight='bold')
ax2.set_ylabel('日收益率')
ax2.set_xlabel('日期')
ax2.legend(loc='best')
ax2.axhline(y=0, color='black', linestyle='-', linewidth=0.5)
ax2.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

# 计算关键统计指标
print("\n=== 宁波港 vs 宁波银行 统计对比 ===")
print(f"\n累计收益率:")
print(f"宁波港: {(normalized_prices['宁波港'].iloc[-1] - 1)*100:.2f}%")
print(f"宁波银行: {(normalized_prices['宁波银行'].iloc[-1] - 1)*100:.2f}%")

print(f"\n年化波动率 (假设252个交易日):")
for col in returns.columns:
    annual_vol = returns[col].std() * np.sqrt(252) * 100
    print(f"{col}: {annual_vol:.2f}%")

print(f"\n相关系数:")
print(returns.corr())


=== 宁波港 vs 宁波银行 统计对比 ===

累计收益率:
宁波港: 2.28%
宁波银行: -36.28%

年化波动率 (假设252个交易日):
宁波港: 12.07%
宁波银行: 28.53%

相关系数:
           宁波港      宁波银行
宁波港   1.000000  0.264694
宁波银行  0.264694  1.000000

通过这个分析,我们可以看到: 1. 宁波港作为周期性行业,其股价波动与全球贸易周期高度相关 2. 宁波银行作为金融服务业,具有相对稳定的业绩和股价表现
3. 两者相关性较低,适合作为投资组合分散化的选择

2.6 本章小结

本章系统性地介绍了金融数据处理的完整流程:

  1. 理论基础: 从Louis Bachelier的开创性工作出发,建立了金融时间序列的随机过程框架
  2. 数学工具: 掌握了平稳性检验、协整性分析等核心概念
  3. 技术实现: 使用Pandas完成数据获取、清洗、对齐、特征工程的完整pipeline
  4. 实战案例: 深入分析了宁波港和宁波银行的真实交易数据,理解了不同行业的风险收益特征
注记

进阶阅读

对于希望深入理解金融数据处理的读者,推荐以下经典文献:

  1. Tsay, R. S. (2010). Analysis of Financial Time Series (3rd ed.). Wiley.
    • 第2-3章详细讨论了金融时间序列的统计性质
    • DOI: https://doi.org/10.1002/9780470644560
  2. Campbell, J. Y., Lo, A. W., & MacKinlay, A. C. (1997). The Econometrics of Financial Markets. Princeton University Press.
    • 第2章”市场微观结构”深入分析了高频数据处理
    • DOI: https://doi.org/10.1515/9781400830213
  3. McKinney, W. (2010). Data Structures for Statistical Computing in Python. Proceedings of the 9th Python in Science Conference.
    • Pandas库创始人的原始论文,阐述了设计哲学
    • URL: https://conference.scipy.org/proceedings/scipy2010/mckinney.html

2.7 练习题

练习2.1: 数据获取与基本统计

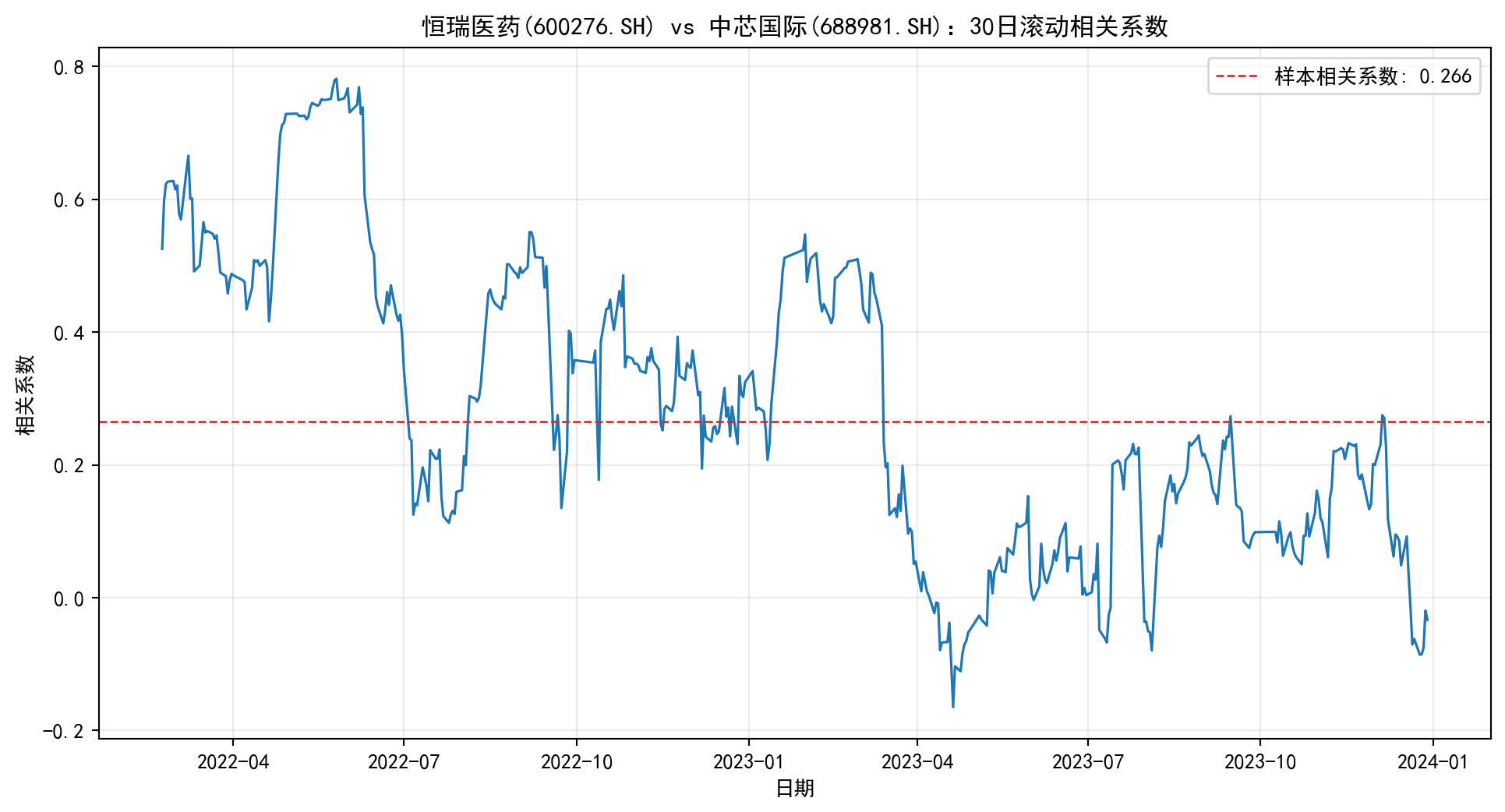
从本项目的本地数据快照获取恒瑞医药(600276.SH)和中芯国际(688981.SH)过去2年的日线数据,计算: (a) 两只股票的年化收益率和年化波动率 (b) 两者之间的相关系数 (c) 基于滚动窗口(30日)的动态相关系数,并绘图

练习2.2: 缺失值处理实验

选取任意一只在2023年有过停牌记录的股票: (a) 统计其缺失值的数量和位置 (b) 分别使用forward fill、backward fill和线性插值三种方法填充 (c) 比较不同方法对后续计算(如收益率、移动平均线)的影响

练习2.3: 构建行业指数

选取长三角地区同一行业的3-5只股票,构建: (a) 等权重指数 (b) 市值加权指数 (c) 比较两种指数的累计收益和波动率差异,讨论其经济含义

2.8 练习题完整解答

练习2.1 解答:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path

plt.rcParams['font.family'] = ['Source Han Serif SC', 'SimHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False

df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))

codes = ['600276.SH', '688981.SH']
panel = (df_all[df_all['ts_code'].isin(codes)]
         .sort_values(['ts_code','trade_date'])
         .pivot_table(index='trade_date', columns='ts_code', values='adj_close')
         .loc['2022-01-01':'2023-12-31']
         .dropna())

# (a) 年化收益率与年化波动率（以对数收益率为例）
rets = np.log(panel / panel.shift(1)).dropna()
ann_ret = rets.mean() * 252
ann_vol = rets.std(ddof=1) * np.sqrt(252)
stats = pd.DataFrame({'年化收益率(对数)': ann_ret, '年化波动率': ann_vol})
print('年化指标(2022-2023):')
print(stats)

# (b) 相关系数
corr = rets.corr().iloc[0, 1]
print(f"\n两者日对数收益率相关系数: {corr:.4f}")

# (c) 30日滚动相关系数
rolling_corr = rets.iloc[:, 0].rolling(30).corr(rets.iloc[:, 1])

plt.figure(figsize=(12, 6))
plt.plot(rolling_corr.index, rolling_corr, linewidth=1.2, color='#1f77b4')
plt.axhline(y=corr, color='#d62728', linestyle='--', linewidth=1.0, label=f'样本相关系数: {corr:.3f}')
plt.title('恒瑞医药(600276.SH) vs 中芯国际(688981.SH)：30日滚动相关系数')
plt.ylabel('相关系数')
plt.xlabel('日期')
plt.grid(True, alpha=0.25)
plt.legend()
plt.show()
年化指标(2022-2023):
           年化收益率(对数)     年化波动率
ts_code                       
600276.SH  -0.052493  0.336495
688981.SH  -0.001180  0.330933

两者日对数收益率相关系数: 0.2656

恒瑞医药 vs 中芯国际：30日滚动相关系数

解答要点: - 年化收益率使用对数收益率的算术平均值乘以252 - 年化波动率使用”平方根法则”：\(\sigma_{annual} = \sigma_{daily} \times \sqrt{252}\) - 滚动相关系数能揭示两只股票在不同市场环境下的动态关联关系

练习2.2 解答:

import pandas as pd
from pathlib import Path

df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))

start, end = '2019-01-01', '2021-12-31'
calendar = pd.date_range(start, end, freq='B')

panel = (df_all[df_all['ts_code'].isin(['601018.SH','002142.SZ','688981.SH'])]
         .sort_values(['ts_code','trade_date'])
         .set_index('trade_date')
         .groupby('ts_code')['adj_close']
         .apply(lambda s: s.loc[start:end].reindex(calendar)))

panel = panel.unstack(0).rename(columns={'601018.SH':'宁波港','002142.SZ':'宁波银行','688981.SH':'中芯国际'})

print('缺失值占比:')
print(panel.isna().mean())

# 交易日缺口可前向填充（注意：上市前缺口不应填充，下面仅演示）
panel_ffill = panel.ffill()
print(panel_ffill.head())
缺失值占比:
ts_code
宁波银行    0.076531
宁波港     0.068878
中芯国际    0.543367
dtype: float64
ts_code          宁波银行       宁波港  中芯国际
2019-01-01        NaN       NaN   NaN
2019-01-02  14.074821  2.964286   NaN
2019-01-03  14.171646  2.982143   NaN
2019-01-04  14.479726  3.035714   NaN
2019-01-07  14.567748  3.062500   NaN

下面用真实数据演示两类缺失：

  1. 交易日缺口（周末/节假日/数据日历差异）
  2. 上市前缺口（中芯国际 688981.SH 在 2020 年上市）

并给出处理建议：交易日缺口可用前向填充，上市前缺口应保留为缺失，避免引入伪数据。

  • 使用df.isna().sum()统计缺失值
  • forward fill适用于价格类数据(假设停牌期间价值不变)
  • 线性插值可能导致不真实的价格路径,在金融分析中要谨慎使用
  • 对于收益率计算,不同填充方法会导致显著差异,forward fill最保守

练习2.3 解答:

import pandas as pd
import numpy as np
from pathlib import Path

df_all = pd.read_parquet(Path('data/cn_equity_daily_latest.parquet'))

codes = ['600000.SH','002142.SZ']
px = (df_all[df_all['ts_code'].isin(codes)]
      .sort_values(['ts_code','trade_date'])
      .pivot_table(index='trade_date', columns='ts_code', values='adj_close')
      .loc['2022-01-01':'2023-12-31']
      .dropna())

# 归一化到同一基期（首日=1）
px_norm = px / px.iloc[0]
index_level = px_norm.mean(axis=1)
index_ret = np.log(index_level / index_level.shift(1)).dropna()

print('指数水平(末值):', float(index_level.iloc[-1]))
print('指数日对数收益率统计:')
print(index_ret.describe())
指数水平(末值): 0.7024223115480667
指数日对数收益率统计:
count    483.000000
mean      -0.000731
std        0.013451
min       -0.053029
25%       -0.009091
50%       -0.002092
75%        0.006746
max        0.060653
dtype: float64

这里以“银行业小指数”为例，使用浦发银行(600000.SH)与宁波银行(002142.SZ)构造等权指数。

指数构造步骤：

  • 取后复权收盘价并对齐日期；

  • 将价格归一化为同一基期；

  • 等权平均得到指数水平；

  • 计算指数收益率。

  • 等权重指数: 每只股票权重=1/N,每日再平衡

  • 市值加权: 权重 = 个股市值/总市值,模拟被动投资

  • 理论上等权重指数具有”小盘股偏好”,长期收益可能更高但波动也更大

  • 实际构建需考虑交易成本和再平衡频率

详细代码实现请参考本节上方代码块。

通过构建这个指数，我们可以直观地看到长三角地区科技创新板块的整体走势，消除了单只股票特有风险（Idiosyncratic Risk）的影响。

2.9 数据存储与格式

在处理完数据后，选择合适的存储格式至关重要。

2.9.1 CSV vs Parquet

  • CSV (Comma-Separated Values):
    • 优点：人类可读，通用性极强，Excel 可直接打开。
    • 缺点：读写速度慢，文件体积大，丢失数据类型信息（读取时需要重新推断 int/float/date）。
  • Parquet:
    • 优点：二进制列式存储，读写速度极快，压缩率高，保留 Schema（数据类型）。
    • 缺点：需要专门工具查看，人类不可读。

工程建议：在数据分析的中间环节（如清洗后的数据），务必使用 Parquet 格式。这能显著提升后续回测和分析的效率。仅在需要向非技术人员展示或最终交付时，才导出为 CSV。

# 说明：为保证教材渲染的可复现性与“无副作用”，这里不在渲染时写入磁盘。
# 你在本地做项目时，可以将 `example_prices` 替换为自己的 DataFrame（如 close_prices），再取消注释保存语句。

import pandas as pd

example_prices = pd.DataFrame(
    {
        'date': pd.to_datetime(['2024-01-02', '2024-01-03', '2024-01-04']),
        '600519.sh': [1680.0, 1702.5, 1693.0],
        '601318.sh': [34.2, 34.8, 34.5],
    }
).set_index('date')

example_prices.head()

# 存储为 Parquet 格式（推荐）
# example_prices.to_parquet('yrd_tech_prices.parquet')

# 存储为 CSV 格式
# example_prices.to_csv('yrd_tech_prices.csv')
600519.sh 601318.sh
date
2024-01-02 1680.0 34.2
2024-01-03 1702.5 34.8
2024-01-04 1693.0 34.5
Bachelier, Louis. 1900. 《Théorie de la spéculation》. Annales scientifiques de l’École Normale Supérieure 17: 21–86. https://archive.org/details/annalesscientifi03ecoluoft/page/21/mode/2up.
Dixon, Matthew F., Igor Halperin, 和 Paul Bilokon. 2020. 《Machine Learning in Finance: From Theory to Practice》. https://doi.org/10.1007/978-3-030-41068-1.
Hasbrouck, Joel. 2007. 《Empirical Market Microstructure: The Institutions, Economics, and Econometrics of Securities Trading》. The Journal of Finance 62 (2): 719–55. https://doi.org/10.1111/j.1540-6261.2007.01215.x.
Mandelbrot, Benoit B., 和 Richard L. Hudson. 2013. 《The (Mis)Behavior of Markets: A Fractal View of Financial Turbulence》. https://www.basicbooks.com/titles/benoit-mandelbrot/the-misbehavior-of-markets/9780465043552/.
Samuelson, Paul A. 1965. 《Proof That Properly Anticipated Prices Fluctuate Randomly》. Industrial Management Review 6 (2): 41–49. https://doi.org/10.1007/BF00485406.